HOME | DD
 duckwagon — Trackpad Tutorial - Mathish Perspective Study
duckwagon — Trackpad Tutorial - Mathish Perspective Study
Published: 2016-06-13 02:19:29 +0000 UTC; Views: 2483; Favourites: 21; Downloads: 0
Redirect to original
Description
So.I've been studying up on my geometry, specifically the 'Classic Constructions' - performing mathematical and geometric functions using only a compass and an unmarked straightedge. Mainly, this is as a study and reference for myself, in trying to understand the mathematical or geometric basis for drawing in perspective. As in, what the principles are that carry across from classic constructions to some of the more advanced perspective drawing techniques.
Also, because it's cool.
Checkitout.
www.mathsisfun.com/geometry/co…
If I can, I'd like to further explore Classic Constructions specifically as they relate to the more advanced Perspective Drawing techniques; as a tool to make perspective drawing easier. If I can understand these things better, I think it will help me be able to use those skills much more naturally.
From what I understand/think, on more mathematical terms: (If only so you can correct me, or otherwise comment.)
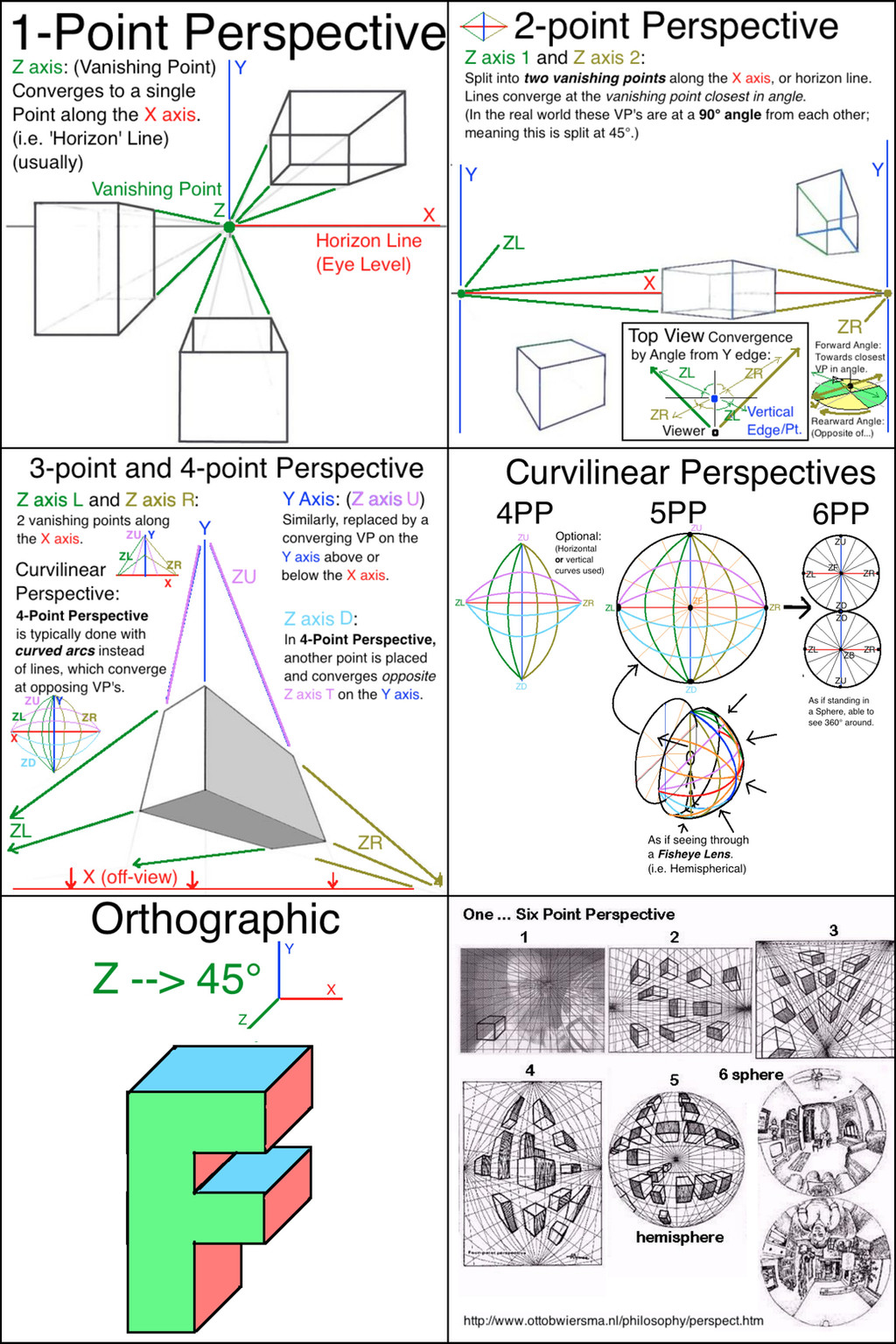
It seems to me that, essentially, a perspective drawing represents more than 2 axes on an flat viewer's plane via vanishing points or planes. (The horizon 'Line' technically being more of a horizontal plane.) I envision this as a sphere surrounding the viewer, with 6 VP's (or 3 cross-sectional planes) at 90° from each other; meaning at exactly top, bottom, front, back, left, and right of you, there is a vanishing point.
In other words: You're flattening the Z-axis down on a XY plane, representing the viewer's point of view; into simplified angles or arcs that converge into vanishing points, or intersecting planes.
In Orthographic perspective, this is simple, with the Z-axis offset by a 45° axis from X and Y.
In Linear perspective, the Z axis is replaced by 1, 2, or 3 convergence points, in face-on 1PP, edge-on 2PP, and vertex-on 3PP views; the X-axis splitting as well in 3pp.
In a sense, I think, you are looking at the subject from inside your sphere, just with the axis planes in a different rotation - i.e. directly towards a single vanishing point; around 45° between two points; and somewhere between 3 horizontal and vertical points; respectively.
This meaning that which point an edge 'converges' towards depends on which vanishing point is closest in angle from the point of view; so a 'rear-pointing' edge will actually also point towards the corresponding opposite VP on front of the sphere. (Does that description make sense? The point to me is that it's technically pointing backward, and thus points transversely across the viewer plane. Left down back = Right up front.)
Curve-Linear perspective takes into account that these aren't straight lines converging at the vanishing points, but a grid of arcs drawn between opposite points, or across intersecting axis planes. 4PP, 5PP, and 6PP essentially stretches the viewing angle farther than (or close to) 2 vp's on the same plane; as if you were looking through a more cylindrical lens, semi-spherical / fisheye lens, or a spherical lens (basically 2 5PP side by side), respectively.
So, With that all in context...
Next comes the real question, and point of this study -
As I understand it, for artistic/proportional congruity purposes, you have to do these sorts of geometric calculations by hand; and the traditional perspective rules and techniques are shorthand for doing specifically that. (Well, you can always take the time sculpting or rendering a full 3d mockup of your subject in some program- which can often mean you have to render a project completely, twice. Yuck. I hate 3d modeling.)
I also realize perspective drawing and 'constructive' drawing have two very different purposes, professionally speaking; perspective focuses on the aesthetic presentation, whereas drafting engineering and the like focus on the functional or informational presentation; thus, typically, they see foreshortening and what-not as (at best) a waste of time, or (more typically) a hindrance to be wary of, against a functional purpose. (At least, from talking with my draftsman dad.)
But (from what I have a hunch about, at least) perspective drawing itself is simply a different way of projecting or flattening the Z axis onto the XY plane; a different way of portraying it. For this reason, I don't think that the geometry an mathematics behind each approach should be any different; so while visually they will function differently, mathematically they function the same way; and maybe you an use the constructive techniques, for a more aesthetic purpose. I fact, I suspect that the perspective techniques taught come from these same principles.
I feel like if I can understand these kinds of geometric constructions better, I might be able to understand and utilize perspective much better in turn; if only to understand why the perspective techniques work for their purposes in the first place. And further, I might even find a few techniques and shortcuts. If it translates.
If that makes any sense.
For example:
Translating proportions or evenly spaced divisions from one segment to another, using parallel lines; in other words, using the transitive (?) property of multiplying triangles.
www.mathsisfun.com/geometry/co…
In perspective drawing, for getting even divisions on an oddly angled line, there is a very similar technique to this. You **(1)** draw a line (b) parallel to the horizon line, connected to one of the end-points of the target segment (a); **(2)** take a vanishing point from the other end of (a) and cross (b), creating a triangle; **(3)** divide line (b) in the correct proportions, and **(4)** take each division point from (b) to the same vanishing point, transferring them to the target line (a).
This works (I think) because the **z axis**, while it visually converges to the vanishing point, is 'technically' considered parallel.
Using both concepts, I can use the geometric construction as part of step 3 above to hopefully smoothen and tighten my workflow.
So what do you think?
I'm thinking of going through the principles discussed in my nifty draftsmanship book, and seeing if I can see the connect between them.
Thoughts?
Am I just behind on my High School geometry from years ago?