HOME | DD
 fractalBuff-ER — Tenth Order Square Julia of the 2^248 Mandelbrot
fractalBuff-ER — Tenth Order Square Julia of the 2^248 Mandelbrot

Published: 2018-01-07 14:37:11 +0000 UTC; Views: 1061; Favourites: 3; Downloads: 0
Redirect to original
Description
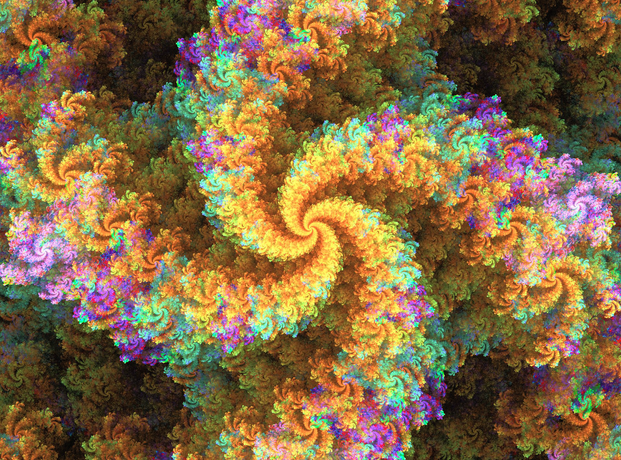
A tenth order Square Julia morphing emanating from the Julia of the first convergence of SethComposerGuy's 2^248 Mandelbrot Zoom: www.youtube.com/watch?v=xqJV3H… . Special care was taken to make the colors as closed to the original palette as possible.The Julia in this image was derived from the Julia morph of the second order inside the real Mandelbrot set (10^157); rendered a Julia with the same seed as the location, and used the Absolute Juliation transformation z = z^2 + c for various foci seven times. Therefore, the zoom in this picture is only 3.141592654 and the iterations used only 110000, but the theoretical zoom is 10^5455 and iterations 17341500.
Seven foci were chosen such that the application of the Juliation transformation z = z^2 + focus will leave thep structure visually unchanged. Julia sets are self-similar precisely because they are invariant under the Juliation transform z = z^2 + seed, based on the identical iteration construction formula, z = z^2 + seed, except the color bands are shifted inward one iteration. The foci are on the Julia's "golden spot", and each Julia has only one golden spot. So, this 4-way tenth order "Julia" Set is actually made of 4096 disconnected Julia sets, each one too small to see, which are arranged and stretched in such a way to make the appearance of a Square "Julia" (e.g. the four heads are of ninth order).
Finally, as the morphing order becomes large (i.e. > 100 times here), the first convergence Julia structure dissolves and only a noisy structure remains with the same seed; disconnection of bands is not imminent because the seed of the first convergence Julia is connected up to 300+ iterations, disconnecting only after a 'latching' second convergence, a Minijulia in the Julia. The last band here has 2048 first convergence Julias (order zero).