HOME | DD
 PosterMasterChef — Graphs Table
PosterMasterChef — Graphs Table
Published: 2012-05-20 15:55:53 +0000 UTC; Views: 2346; Favourites: 34; Downloads: 56
Redirect to original
Description
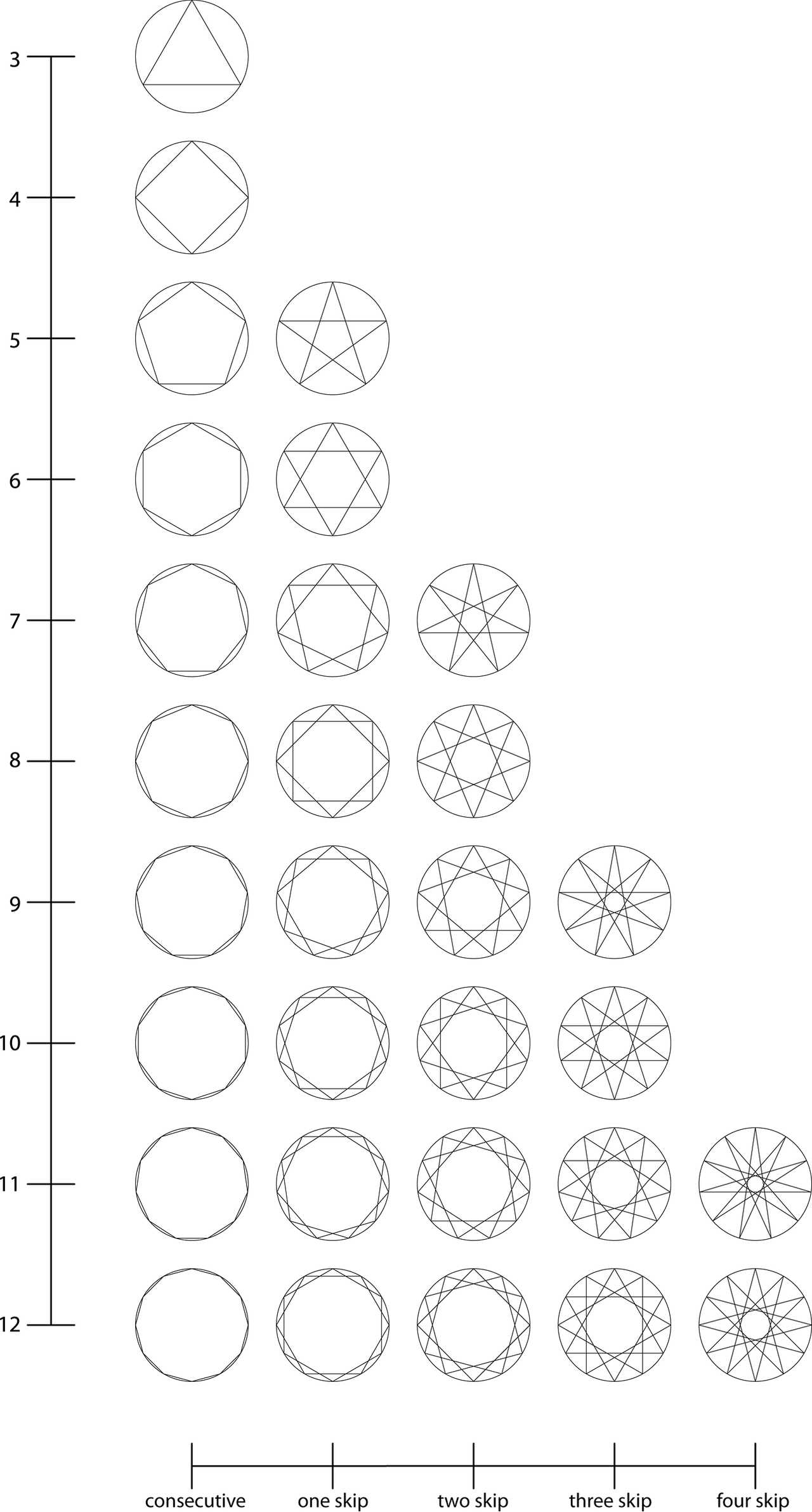
Here is the table of all graphs (from three to twelve vertices) inscribed in a circle.In the first column the connection between vertices is consecutive, in the second is skipped one vertex, in the third two vertices, and so on.
The rows are not completely filled: if I had continued, skipping more vertices, I regained the same graph (In cases of an even number of vertices, before the same graphs I obtain crosses).
Is interesting to note that if the number of vertices of a graph has dividers, some of the graphs obtained are composed of multiple polygons.
For example: The dodecagon has 12 vertices, twelve is divisible by two, three and four, and in fact one of the graphs I get is composed of two hexagons, one by three square, and one by four triangles.
I've posted it in png so if someone wants use one of them he can do it. only quote me!