HOME | DD
 Audiazif — How to Draw Squares in Perspective
Audiazif — How to Draw Squares in Perspective
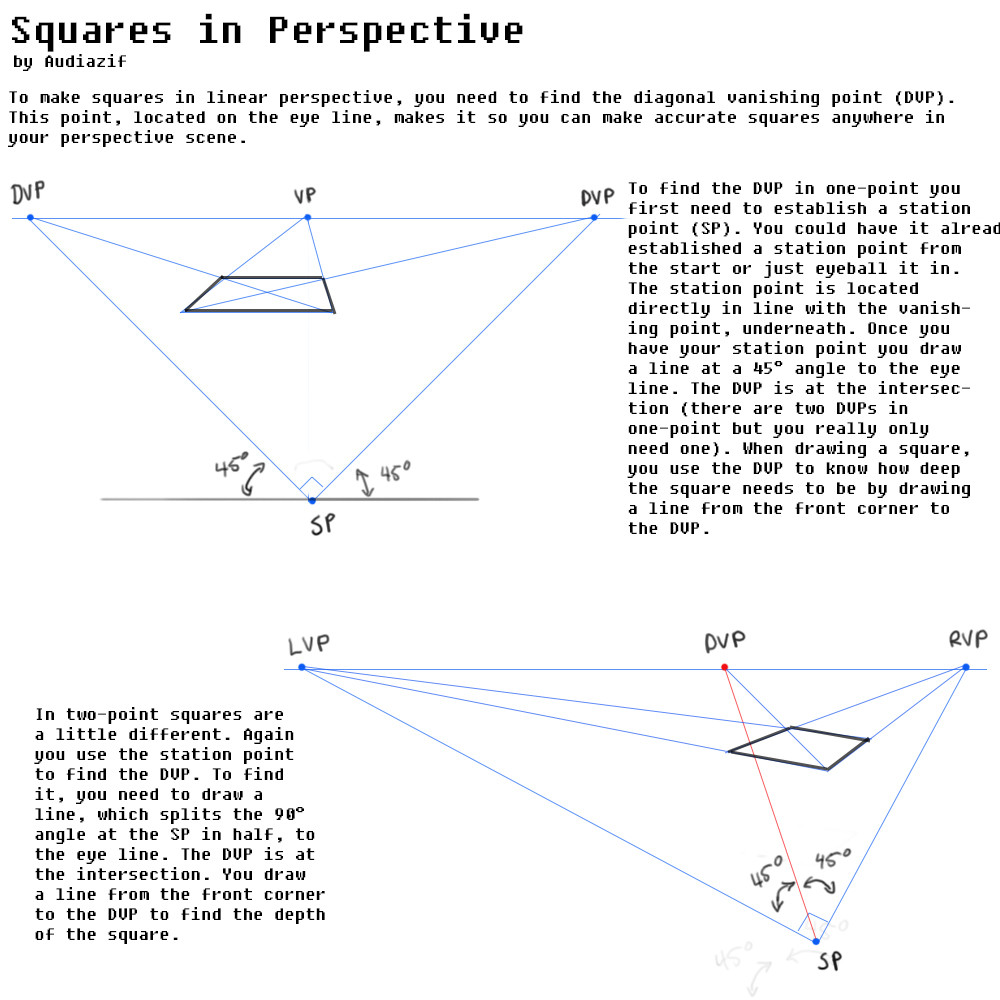
#drawing #drawings #drawingtutorial #howto #howtodraw #perspective #tutorial #tutorials #howtopaint
Published: 2015-08-31 06:10:30 +0000 UTC; Views: 2788; Favourites: 22; Downloads: 0
Redirect to original
Related content
Comments: 3

Thank you! It is very helpful.
But is there a way to calculate the distance from SP to VP in one-point perspective? Otherwise it is just very subjective.
On the second thought, SP in two-point can also be anywhere since there are infinite number of points of SP that make 90° with LVP and RVP.
I don't understand it yet, can you explain the concept in detail?
👍: 0 ⏩: 1

Ok i will try my best.
Let me address the infinite possibilities for sets of points at 90° to the SP in two-point. The SP (station point) represents the point where the viewer is standing and it never moves once setup. You are correct that there are infinite number of sets of points but since the SP doesn't move the different sets of points changes the orientation or rotation of the objects.
As for the distance between SP and VP in one-point, I'm sure there is some complicated way using geometry, trig, and calculus to find the exact distance but imo it is not worth it (and tbh I have no clue how). Now I have learned a few simple tricks that may work. The quick and dirty solution would be to take the distance from the eye line to the top of you picture plane and the SP would be that distance from the bottom of the picture plane. Another thing that can determine the distance, in one-point and two-point, is the cone of vision (aka field of view). Also like I said in the tut you could already have the Sp set up, once you have the SP setup it limits where you can put objects because no objects can be behind the SP. Or the last trick would be just to wing it. After drawing a lot of perspective you will learn shortcuts around complicated set ups and you will know what probably looks right.
I hope this helps.
👍: 1 ⏩: 1

Thank you. I actually think that I'm not that bad at guessing the perspective. I just don't like being unable to find the answer.
So I found it. It looks like the distance from SP to the horizon line always equals the radius of your circle of view. The "circle of view" is not very specific, but if we take the more or less detailed field of view for 90°, it looks about right. Note that the circle of view ≥ your picture. I found it in some architecture article/tutorial, so guess it's as precise as it can be.
👍: 0 ⏩: 0