HOME | DD
 FractalMonster — Blowing
by-nc-sa
FractalMonster — Blowing
by-nc-sa

Published: 2008-06-18 13:35:06 +0000 UTC; Views: 1095; Favourites: 33; Downloads: 40
Redirect to original
Description
Updated to 1960x1470 resolution when downloaded
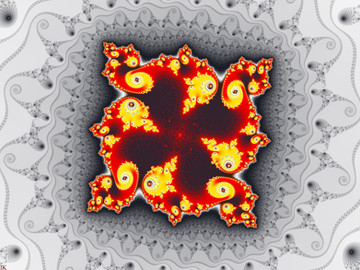
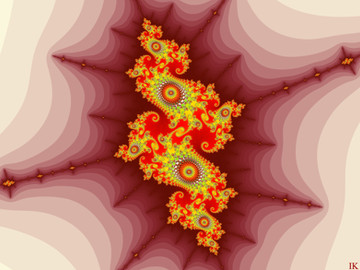
This motive comes from a couple of in-zooms in the disconnected regions to the left in CubeQuadraticConfussion1b (best viewed in this version).
It is a part of a 2d-slice of the six dimensional 
*a_real = 0.5
*a_imag = 0
*b_real = 0.5
*b_imag = 0
*c_real = #pixel (horizontal)
*c_imag = #pixel (vertical)
The set M1, totally identical with M2, is drawn in one layer and M3 is drawn in the other layer. It’s the set M1 = M2 that forms the contour ot the cubic Mandelbrot set
Ultra Fractal, formula Quartic Parameterspace3 in the sp3-module written by my dear friend Stig Pettersson, Greenseng here at DeviantART. All his modules, as well as mine can be downloaded from klippan.seths.se/fractals/arti…
No filters or postprocessing
Below the UF parameter file, play and have fun
Blowing {
fractal:
title="Blowing" width=800 height=600 layers=2
credits="Ingvar Kullberg;6/5/2018"
layer:
caption="M1=M2" opacity=100 mergemode=difference method=multipass
mapping:
center=-0.115640456113215/-6.8513737092e-7 magn=9122.2582
formula:
maxiter=50000 filename="sp3.ufm" entry="QuarticParameterspace3"
p_PlottedPlane="15.(c-real,c-imag)" p_M=M1 p_SetBorders=no
p_hide=yes p_areal=0.5 p_aimag=0.0 p_breal=0.5 p_bimag=0.0
p_creal=0.0 p_cimag=0.0 p_xrot=0.0 p_yrot=0.0 p_xrott=0.0
p_yrott=0.0 p_xrotu=0.0 p_yrotu=0.0 p_xrotv=0.0 p_yrotv=0.0
p_zrot=0.0 p_LocalRot=no p_diff=no p_bailout=100.0 p_dbailout=1E-6
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes index=9 color=327680 index=40 color=15794175 index=52
color=655360 index=107 color=16769274 index=187 color=2445567
opacity:
smooth=no index=0 opacity=255
layer:
caption="M3" opacity=100 method=multipass
mapping:
center=-0.115640456113215/-6.8513737092e-7 magn=9122.2582
formula:
maxiter=50000 filename="sp3.ufm" entry="QuarticParameterspace3"
p_PlottedPlane="15.(c-real,c-imag)" p_M=M3 p_SetBorders=no
p_hide=yes p_areal=0.5 p_aimag=0.0 p_breal=0.5 p_bimag=0.0
p_creal=0.0 p_cimag=0.0 p_xrot=0.0 p_yrot=0.0 p_xrott=0.0
p_yrott=0.0 p_xrotu=0.0 p_yrotu=0.0 p_xrotv=0.0 p_yrotv=0.0
p_zrot=0.0 p_LocalRot=no p_diff=no p_bailout=100.0 p_dbailout=1E-6
inside:
transfer=none
outside:
transfer=linear
gradient:
smooth=yes index=9 color=657930 index=48 color=16777205 index=104
color=655360 index=142 color=16724058
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 14

haha, everytime I watch your gallery I find something new I like...
this is awsome!
👍: 0 ⏩: 1

I am really honored :blushed: Most of my fractals are parts of a big journey into the big mystery 

👍: 0 ⏩: 1



👍: 0 ⏩: 1

Heard of it in convosation but I'm not realy clear
👍: 0 ⏩: 1

Then below some recycled info
Wikipedia has a nice site [link] 

Regarding deep zooms in the Mandelbrot set, if you check out my deviation "Cauliflowerfort" [link] and click the link under "Artist's Comments" you can follow the entire zoom sequence in 28 steps
In my journal [link] you have some link to short cool fractal animations I stumbled over at YouTube 
👍: 0 ⏩: 1

thanks. the information on wikipedia is interesting :3
👍: 0 ⏩: 1

You may have the links as a resource
👍: 0 ⏩: 1

Thank you Frank 

👍: 0 ⏩: 0