HOME | DD
 FractalMonster — Inside Out
by-nc-sa
FractalMonster — Inside Out
by-nc-sa
Published: 2007-05-27 13:43:49 +0000 UTC; Views: 1601; Favourites: 15; Downloads: 16
Redirect to original
Description
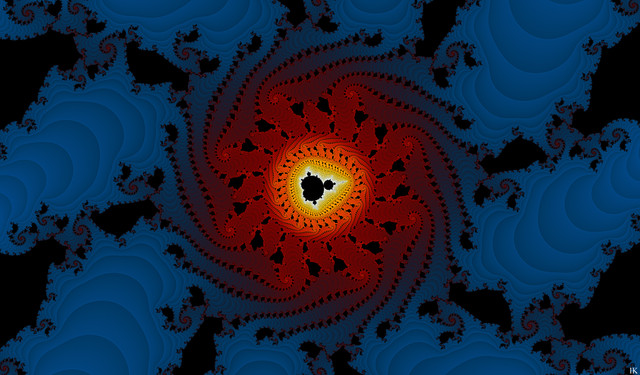
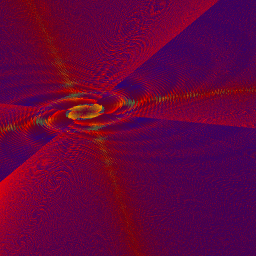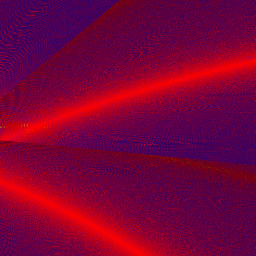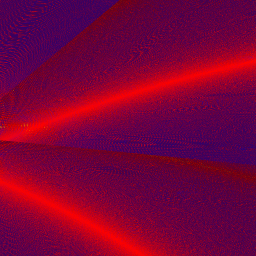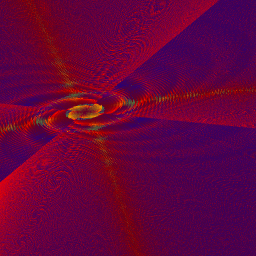
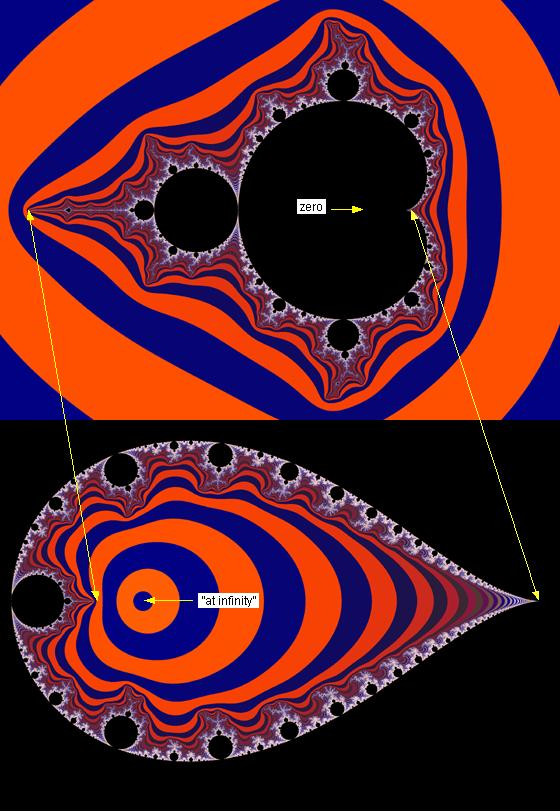
Turning the Mandelbrot set inside outor
When zero and infinity alter their places
Full view please for the illustration
The upper half of the illustration is generated by the dynamical process z -> z^2 + c when the variable “z” is initiated to zero and “c” varies with the pixels (c = # pixels). The black part is the Mandelbrot set and is constituted of those “c” for which “z” under iteration stays forever within a radius of 2 from the center of the dynamical (z-) plane. The surrounding colors are settled according to how many iterations (how many times the variable “z” has to pass the loop) for the corresponding “c” before “z” passes a radius of at least two, in this image 10, and thus escapes to infinity. But all of this is much more clearly described in articles 1 – 9 in my Chaotic series of fractal articles.
Now we shall perform a little joke. We let the infinity and zero on the parameter plane (the c-plane) alter their places. That means we turn the parameter plane (containing the M set and the surrounding level sets) inside out by instead iterating z -> z^2 + 1/c. The result is shown in the lower part of the illustration, the black set is the Inverse Mandelbrot set. that now surrounds the level sets in the central part of the image. Note that there are one-to-one correspondences between every point in the upper and lower planes if they are extended to include the infinity. In fact the border of the sets are exactly similar, the branches of the Inverse M set containing copies of ordinary M set in exactly the same way the ordinary M set does. The double arrowhead lines show this.
This “inside-out-process” throw away the “zero” in the upper motive to infinity’s infinity in any direction in the lower image and, at the same time, catches the infinity’s infinity in any direction in the upper image and places it on the well defined spot “at infinity” in the lower image. But all this has partly to do with the mysteries of zero divides, see my preceding journal The mysteries of zero divides







And when the space is turned inside out, the whole universe will be situated inside you







Related content
Comments: 121

Hehe not yet, but maybe we are all on the way towards the infinity
👍: 0 ⏩: 1

The infinity... sounds cool
👍: 0 ⏩: 1

Sometimes it maybe gonna be to cool
👍: 0 ⏩: 1

No, nothing can ever be too cool. 

👍: 0 ⏩: 1

Well, I do like to take on new challenges
👍: 0 ⏩: 1

We ought to take that, even if we don't know in which direction we leave for infinity
👍: 0 ⏩: 1

wow! det där måste jag testa.
en fråga bara, om man rör sig ifrån oändligheten, komer man närmare och närmare 0 utan att komma fram helt och hållet? (med en endring som avtar exponensiellt?)
bara nyfiken
rolig ide dock
fortsätt komma med om inlägg spännande mattematik!
Ha det bra Ingvar!
👍: 0 ⏩: 1

Kanske snarare en fråga om man någonin kommer närmare oändligheten 
Vet inte om detta var något bra svar 

👍: 0 ⏩: 0

Pure genius. Completely incomprehensible to my feeble intelligence, but, pure genius!
👍: 0 ⏩: 1

Well, if you meditate on the illustration above (in full view) you will get an intiutive opinion what I've tried to explain 
..and thank you for your kind words
👍: 0 ⏩: 1

Actually, I do get it. Er, ok, the math . . . not so much. But your little scrap explanation just moved me lightyears ahead in my understanding of how my fractal generator works. Now I'm messing around with the equations behind the scenes rather than just zooming in through dwells to find something cool. Thank you for sharing, both your wonderful gallery and your knowledge.
👍: 0 ⏩: 1




Maybe you can try my chaotic series [link] . Not all articles are of mathematical nature, for example articles 10 - 14
👍: 0 ⏩: 1

I just spent about 3 hours working through your website and links to other manuals. WOW! When my brain clears, I'm gonna feel so smart
Thank you.
👍: 0 ⏩: 1

Well, hope it did not destroyed your afternoon 

- Complex numbers (basic knowledge),
- Iteration,
- The difference between Julia sets and the Mandelbrot set (including the analogies for higher polynomials)
BTW, what software do you use?
👍: 0 ⏩: 1

Destroy?? Not at all. I got into it and before I knew the afternoon had been spent. . . very well I might add. I can't wait to get home and start working with my son with this stuff. He loves math and fractals are the ultimate visual math.
I use several shareware fractal apps, Fractal Domains being chief among them. I also primarily use Mac OSX.
👍: 0 ⏩: 1




👍: 0 ⏩: 1
<= Prev |