HOME | DD
 FractalMonster — Inside Out
by-nc-sa
FractalMonster — Inside Out
by-nc-sa
Published: 2007-05-27 13:43:49 +0000 UTC; Views: 1601; Favourites: 15; Downloads: 16
Redirect to original
Description
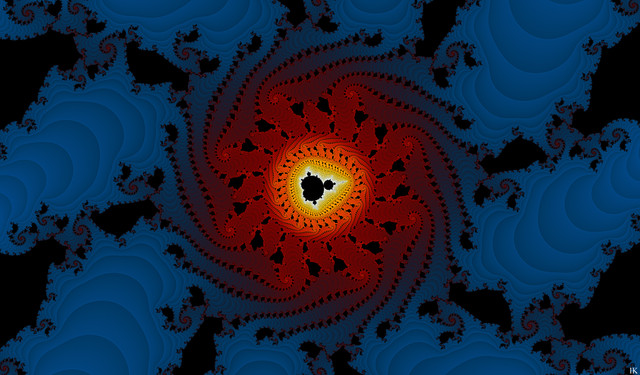
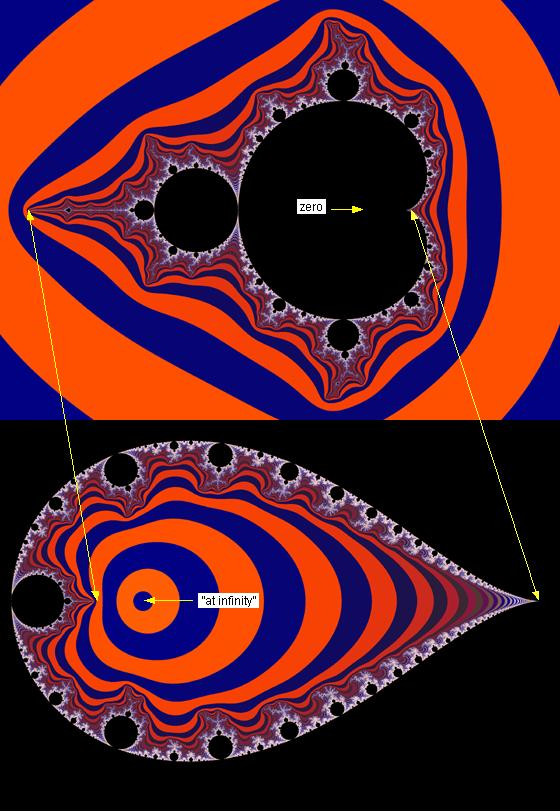
Turning the Mandelbrot set inside outor
When zero and infinity alter their places
Full view please for the illustration
The upper half of the illustration is generated by the dynamical process z -> z^2 + c when the variable “z” is initiated to zero and “c” varies with the pixels (c = # pixels). The black part is the Mandelbrot set and is constituted of those “c” for which “z” under iteration stays forever within a radius of 2 from the center of the dynamical (z-) plane. The surrounding colors are settled according to how many iterations (how many times the variable “z” has to pass the loop) for the corresponding “c” before “z” passes a radius of at least two, in this image 10, and thus escapes to infinity. But all of this is much more clearly described in articles 1 – 9 in my Chaotic series of fractal articles.
Now we shall perform a little joke. We let the infinity and zero on the parameter plane (the c-plane) alter their places. That means we turn the parameter plane (containing the M set and the surrounding level sets) inside out by instead iterating z -> z^2 + 1/c. The result is shown in the lower part of the illustration, the black set is the Inverse Mandelbrot set. that now surrounds the level sets in the central part of the image. Note that there are one-to-one correspondences between every point in the upper and lower planes if they are extended to include the infinity. In fact the border of the sets are exactly similar, the branches of the Inverse M set containing copies of ordinary M set in exactly the same way the ordinary M set does. The double arrowhead lines show this.
This “inside-out-process” throw away the “zero” in the upper motive to infinity’s infinity in any direction in the lower image and, at the same time, catches the infinity’s infinity in any direction in the upper image and places it on the well defined spot “at infinity” in the lower image. But all this has partly to do with the mysteries of zero divides, see my preceding journal The mysteries of zero divides







And when the space is turned inside out, the whole universe will be situated inside you







Related content
Comments: 121

"And when the space is turned inside out, the whole universe will be situated inside you"
Aaaah! Light begins to dawn now.
👍: 0 ⏩: 1

This is somewhat related to [link]
👍: 0 ⏩: 0


BTW, also check out [link]
👍: 0 ⏩: 1

Thinking about them as objects or sets it is interesting.
I am not sure if they are infinite; maybe not?
Thanks
👍: 0 ⏩: 1

That's the approach I always have. At least the borders have infinite length (as the borders are fractals) 
👍: 0 ⏩: 1

Yeah 
..and when we turn the M set inside out, we catch the infinity and place it in the well defined point "at infinity" in the center of the coordinate system, the spot where the zero was before the "inside-out" operation
A big mystery: From which direction did we catch the infinity, and in which direction did we throw away the zero when we throw it to infinity
👍: 0 ⏩: 1

I have the book of Mandelbrot next to me.
It says 'gli oggetti frattali', forma,caso e dimensione.
Here is talking about a certain Koch..page 30..
You make the thing more interesting!
👍: 0 ⏩: 1

Sounds like "The Fractal Geometry of Nature" which I got for some years ago
👍: 0 ⏩: 0

Hey, that does make sense if you put it into perspective hmmm.. Me like
Em xx ♥
👍: 0 ⏩: 1

Thank you 
👍: 0 ⏩: 1

Ahh okk. Cool.
Em xx ♥
👍: 0 ⏩: 1

Yeah, isn't 
👍: 0 ⏩: 1

Wow, I could stare at it for hours! @_@
👍: 0 ⏩: 1

Then you'll be transcended into infinity
👍: 0 ⏩: 1

I could finally read all the books I want to read and design all the fractals I want to make!
👍: 0 ⏩: 1

Well, then you must be a "time millionaire" 
👍: 0 ⏩: 1

It's nice to be a millionaire of some kind!
👍: 0 ⏩: 1

Yeah 
👍: 0 ⏩: 1

Oh wow I like the way u presented this 

👍: 0 ⏩: 1

Really glad you appreciate it 
👍: 0 ⏩: 1



👍: 0 ⏩: 1




👍: 0 ⏩: 1

LOL 



👍: 0 ⏩: 1

Learned more American English tonight 
👍: 0 ⏩: 1

Wow thats really awesome! I wish I could do that - Turn inside out ^^
👍: 0 ⏩: 1

Yeah, when zero plays with infinity everything could happen
👍: 0 ⏩: 1


👍: 0 ⏩: 1

Hehe, the zero an the infinity are perhaps the only entities the neglegt any barriers
👍: 0 ⏩: 1

I like zero ^^ we introduced it to the world after all *is very proud* lol :wink: I'm trying to be all pompous hehe!!
👍: 0 ⏩: 1

You are aloowed to be 
👍: 0 ⏩: 0

...and you are not afraid being turned inside out 
Thank you Kathi
👍: 0 ⏩: 1

its never bothered me before (grin)
👍: 0 ⏩: 0

I also 
👍: 0 ⏩: 0

Yeah, isn't it 
👍: 0 ⏩: 1

great apo-master?
👍: 0 ⏩: 1

Yeah, I think you to be so 
👍: 0 ⏩: 1


👍: 0 ⏩: 1
| Next =>