HOME | DD
 FractalMonster — The Limitation Dissolves
by-nc-sa
FractalMonster — The Limitation Dissolves
by-nc-sa
#compass #exponent #formula #play
Published: 2019-06-08 11:15:45 +0000 UTC; Views: 583; Favourites: 32; Downloads: 10
Redirect to original
Description
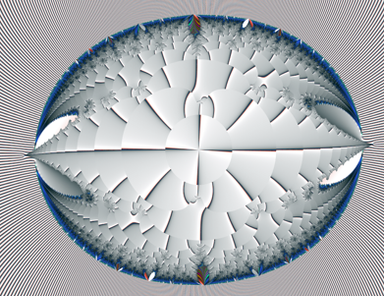
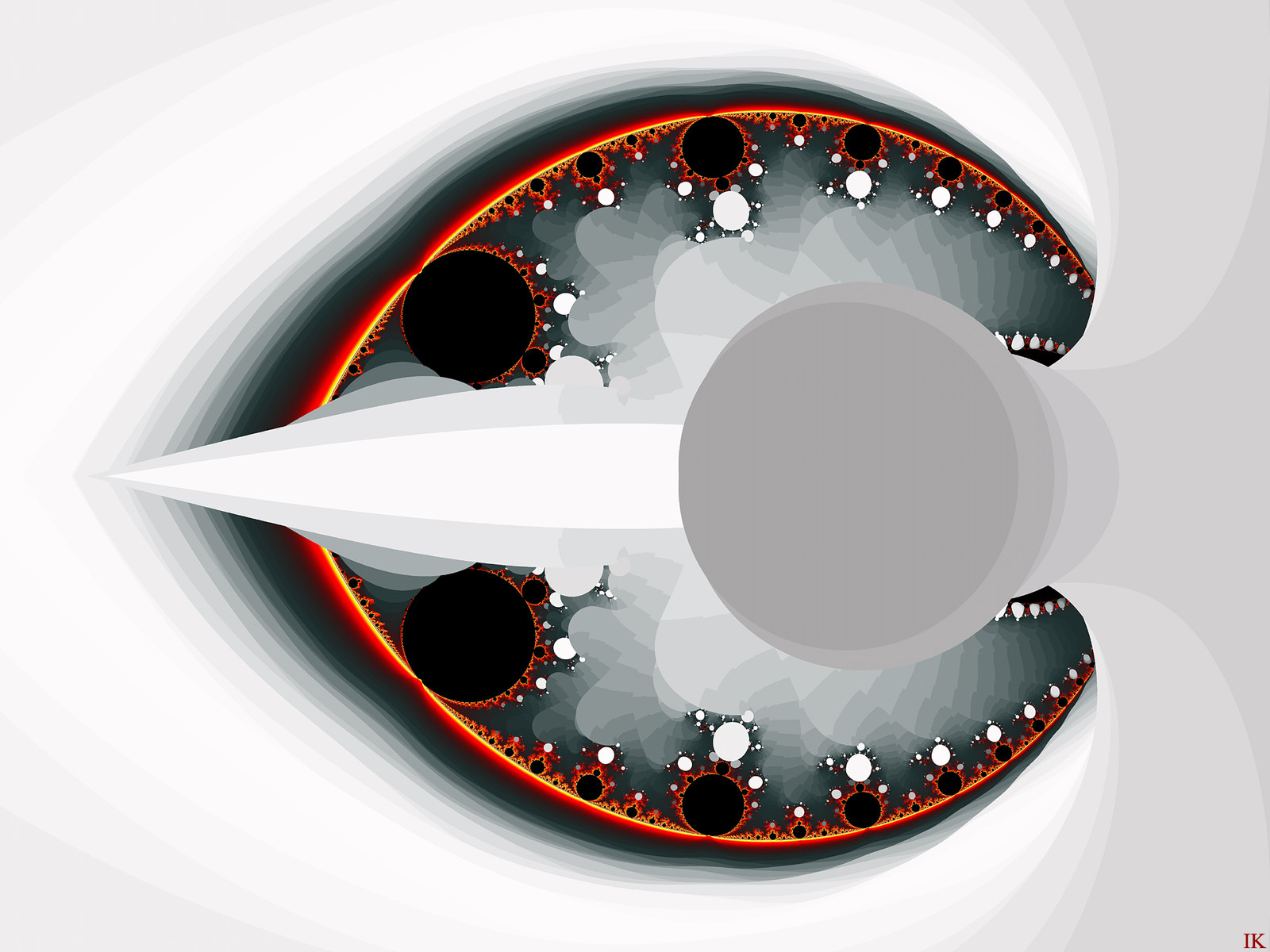
Playing with the exponent in my compass formula, z -> z^d - da^(d-1) z. See my journal Fractal CompassesNow, my dear readers, I wanna promote the article,27) Compasses
in my Chaotic series. Along with this journal there are four deviations uploaded,
Compass_d=2
Compass_d=3
Compass_d=4
Compass_d=5
The “d” is the exponent in the iterated polynom p(z) = z^d - da^(d-1) z, the a-plane plotted and “z” initialized to the critical point z = +a. Why this formula is called the “Compass formula”? Well, just look at the above deviations, especially for d = 3 and higher






 For d = 3 we actually have z^3 - 3a^2 z whic
For d = 3 we actually have z^3 - 3a^2 z whic 






The exponent "d" in this motive is set to 0.875+0i.
Also playing with Diff-bailout coloring 1-periodig components according to the number of iterations required to take the variable to a fix point.
This routine in htese images also give rise to artifacts which is used by me in these images, the artifacts depending of the Dbailout ..
Software: Ultra Fractal.
Formula: Extended Compasses (adding a parameter "b". the full parameter space becoming a four dimensional hyper space).
TheLimitationDissolves {
fractal:
title="The Limitation Dissolves" width=800 height=600 layers=1
credits="Ingvar Kullberg;5/18/2019"
layer:
caption="Background" opacity=100 method=multipass
mapping:
center=-8.7356598285862457985e-11/0 magn=7.338366E9
formula:
maxiter=10000 percheck=off filename="ik3.ufm"
entry="ExtendedCompasses" p_exponent=0.875/0
p_PlottedPlane="1.(a-real,a-imag)" p_hide=yes p_areal=0.0
p_aimag=0.0 p_breal=0.0 p_bimag=0.0 p_xrot=0.0 p_yrot=0.0
p_xrott=0.0 p_yrott=0.0 p_zrot=0.0 p_LocalRot=no p_diff=yes
p_bailout=10000000 p_dbailout=1E-20
inside:
transfer=none
outside:
density=0.1 transfer=linear
gradient:
smooth=yes rotation=-125 index=5 color=16579582 index=14
color=3026462 index=54 color=223 index=72 color=255 index=-249
color=57075 index=-38 color=16777212 index=-7 color=1709847
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 8



👍: 0 ⏩: 1

Sorry for slow response. Yes I have just gotten into fractals. I use them a lot in my art in instagram..
👍: 0 ⏩: 1

OK 

(if the links to my external pages don't work, check out this journal)
Maybe you would appreciate my Chaotic series of fractal articles (<- click) if you have a little theoretical interest 
Regarding deep zooms in the Mandelbrot set, if you check out my deviation Cauliflowerfort and click the link under "Artist's Comments", from page 4 you can follow the entire zoom sequence in 28 steps 
In this journal you have some links to cool fractal animations I stumbled over at YouTube. Also check out the zoom videos in this journal 
.. and from the middle of the nineties there is a fantastic TV program about fractals, Colors of Infinity by Arthur Clarke 

(the above info is recycled)
👍: 0 ⏩: 1

Wow! Thanks a lot!
👍: 0 ⏩: 1

My pleasure 
👍: 0 ⏩: 0

Dangerous to the fractal
👍: 0 ⏩: 0