HOME | DD
 FractalMonster — Weird Barriers13
by-nc-sa
FractalMonster — Weird Barriers13
by-nc-sa

#mandelbrot #set
Published: 2014-10-27 19:43:15 +0000 UTC; Views: 429; Favourites: 15; Downloads: 18
Redirect to original
Description
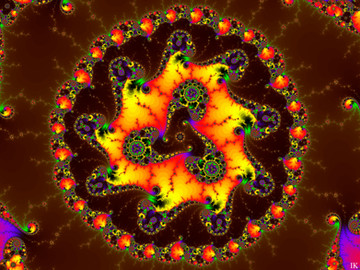
Deep in-zoom in the right lower flank ofSoftware: Kalles Fraktaler. Se my journal,
New Revolutionary Algorithm for the Mandelbrot set (updated)







Formula: The standard Mandelbrot formula (z -> z^2 + c).
Magnification: 1.79999999995x10^132
Coordinates:
Re: 1.253159674610968788433574193858451459400437487272399303687670434047014663791573840733948190293921588825380670431972928220858257109044458891539586524188585
Im: -0.04650101233451811929191912556074791410857738704790140011156999853142232814940633191176328258065765400915097548131761969637541509742258561064800080263589
Related content
Comments: 19

Nice work! I consider that location need less different colors and histogram equalization like in Mandel Machine.
P.s. reminds my Julia Julia Set. You have invited another Julia Evolution. Congrandulations!
👍: 0 ⏩: 1

Mandel :machine I've failed to install 

👍: 0 ⏩: 2

MM... If you want to setup it, write me in Skype: mstrkrft_xxl
I'll answer you on all MandelMachine questions in chat. Your choice.
👍: 0 ⏩: 1

Sorry I have no Skype (and no fb either). But thanks
Is MM much better than FK? I've just got a little bit hang of the color editor of that software no 
👍: 0 ⏩: 1

Mandel Machine support palettes to. You should have only Jpeg, png or bmp image with palette. mandel Machine interpolate it to millions colors. This is very fast program for explore smth and rendering images with any coloring technique, like a Ulrta Fractal (transfer functions - log, root, cube root, correct Histogram Equalization etc.)
👍: 0 ⏩: 1

Yeah, I heard that MM is even faster than KF 
👍: 0 ⏩: 1

Now I render 10240x5760 (16:9) frames for new video. Some frames is very long to wait (182 frames, really!). I render it for a month. But end is near ^_^
👍: 0 ⏩: 1



👍: 0 ⏩: 1

Yes! Zoom is 2^181 but 182 frames needed + waiting so much time! Of course, maximum iterations is 20,000,000-100,000,000!!!
👍: 0 ⏩: 1

.. and I often wonder why magnifications are written in the potents of 2 
👍: 0 ⏩: 1

You can try to render every e10 and you'll see worse quality!!!
👍: 0 ⏩: 1

Your article written correctly! Now I have a question: why I do this (explore the M-Set)??? Sometimes, friends ask me this...
👍: 0 ⏩: 1

I hope so 
👍: 0 ⏩: 1

Yes, I'll write article about M-Set too)))
👍: 0 ⏩: 1