HOME | DD
 MathMod — Gyroidal Torus
MathMod — Gyroidal Torus
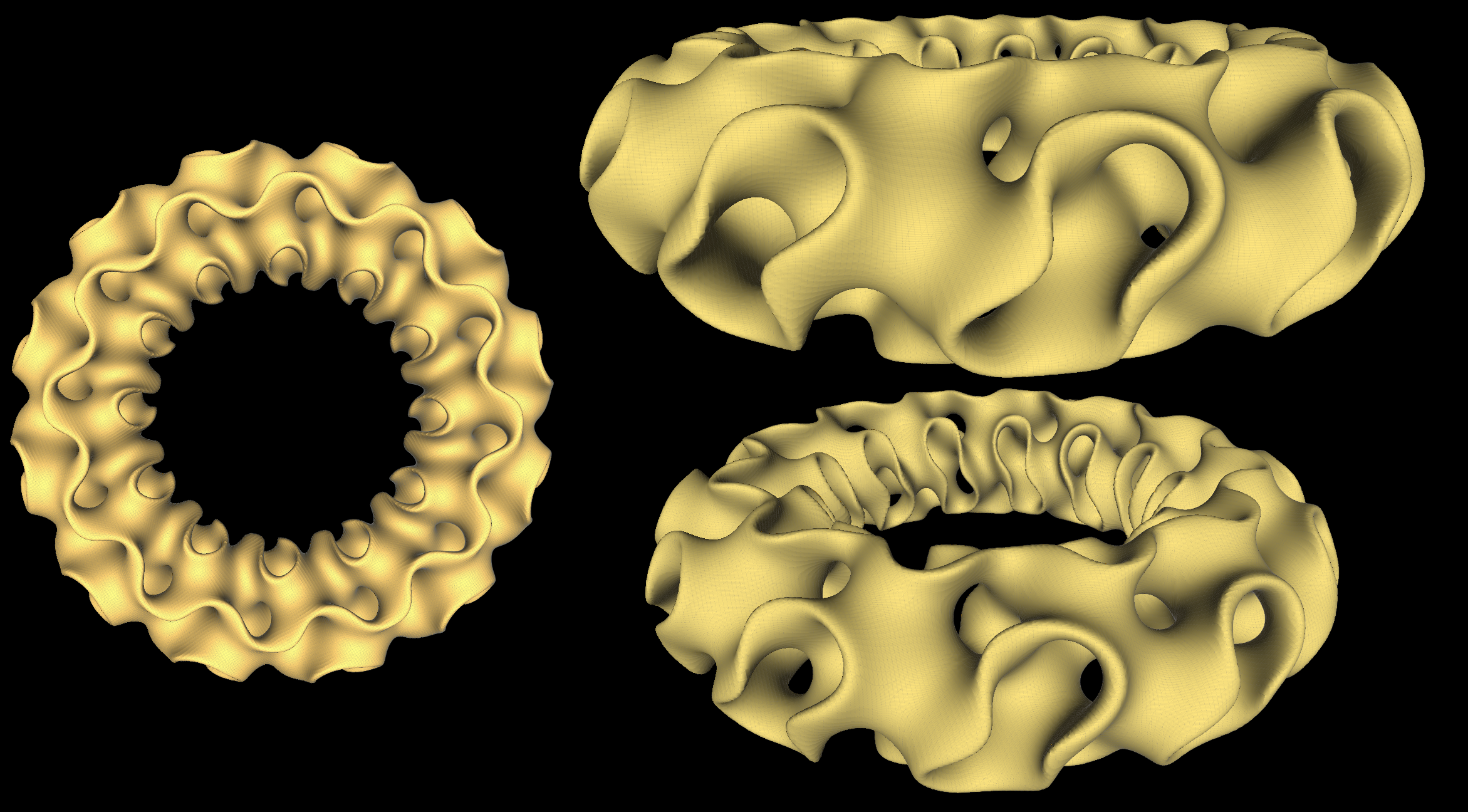
#3d #mathematics #mathmod
Published: 2015-11-23 00:55:38 +0000 UTC; Views: 722; Favourites: 2; Downloads: 2
Redirect to original
Description
Gyroidal TorusThe Gyroidal Torus is the result of bending a cylinder filled with a gyroidal "thick" surface.
MathMod script:
{
"Iso3D": {
"Description": ["Gyroidal Torus-1.2 by Abderrahman Taha 21/11/2015"],
"Name": ["Gyroidal Torus"],
"Component": ["GyroidalTorus"],
"Const": ["cx=0.0001",
"cy=0.0001",
"cz=0.0001"],
"Funct": ["Iso=cos(x)*sin(y)+cos(y)*sin(z)+cos(z)*sin(x)",
"Tickness2= (.4)",
"DFx= ((Iso(x,y,z,t)-Iso(x+cx,y,z,t))/cx)",
"DFy= ((Iso(x,y,z,t)-Iso(x,y+cy,z,t))/cy)",
"DFz= ((Iso(x,y,z,t)-Iso(x,y,z+cz,t))/cz)",
"Rapport= (sqrt(DFx(x,y,z,t)*DFx(x,y,z,t)+DFy(x,y,z,t)*DFy(x,y,z,t)+DFz(x,y,z,t)*DFz(x,y,z,t)))",
"Iso4= (Iso(x-DFx(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),y-DFy(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),z-DFz(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),t))",
"Iso5= (Iso(x+DFx(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),y+DFy(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),z+DFz(x,y,z,t)*Tickness2(x,y,z,t)/Rapport(x,y,z,t),t))",
"TickIso2= (Iso4(x,y,z,t)*Iso5(x,y,z,t))",
"isoCondition= (x^2+z^2-16)",
"isoTransform_1=if(isoCondition(x,y,z,t)<0,TickIso2(x,y,z,t),1)+exp(isoCondition(x,y,z,t)/3)"],
"Fxyz": ["isoTransform_1((sqrt(x*x+y*y)-10),12*atan2(y,x),z,t)"],
"Xmax": ["14"],
"Xmin": ["-14"],
"Ymax": ["14"],
"Ymin": ["-14"],
"Zmax": ["4"],
"Zmin": ["-4"]
}
}
Related content
Comments: 6

Very nice, I think I produced some similar shapes in k3dsurf by hacking formulae together, but with nowhere near as much elegance and finesse as these.... Thanks!
Jason
👍: 0 ⏩: 1

Thank you! 
MathMod was developed with the main idea of pushing the math exploration a bit further than what we can do with K3DSurf .
From what I know, there still a lot more to discover...
👍: 0 ⏩: 0

Yes, it is - this is awesome!
Thank you so much for providing those great shapes to explore!
👍: 0 ⏩: 1

Had some fun and played with the formula - did a simple render
schmiegel.deviantart.com/art/G…
Thanks again!
👍: 0 ⏩: 1

Wow! very beautiful work
I've also played with it and used the Schwarz minimal surface instead of the Gyroid: mathmod.deviantart.com/art/Sch…
👍: 0 ⏩: 0
















