HOME | DD
 MathMod — Inka Sun
MathMod — Inka Sun

#3d #mathematics #mathmod
Published: 2015-10-15 03:23:43 +0000 UTC; Views: 402; Favourites: 1; Downloads: 0
Redirect to original
Description
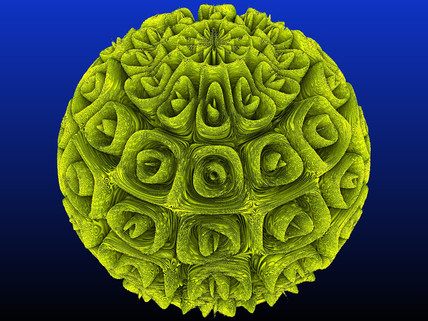
Inka Sun (parametric model)As seen in these two models,there is an infinite possibilities of carving the Torus (and other mathematical models)...
Very promising results especially for people interested in printing 3D mathematical models because MathMod can export to .OBJ file format all it's models.
--------------
Update:
--------------
Here is it, the script to generate the "Inka Sun" and Carl Sequin cutted Toroids models.
By default, the attached model will cut the Torus to three Toroids.
You can set the number of Toroids with the parameter N (there is virtually no limit except the resolution of your model).
1) To generate the "Inka Sun", replace :
"Tickness1=if( t = 1, if ( (abs(sin((N/2)*u-v)))>.38,-.45,0),if ( (abs(sin((N/2)*u-v)))<.38,-.45,0))",
by
"Tickness1= if(if(t=1,(abs(sin((N/2)*(u*(sin(v))-u))))<.4,(abs(sin((N/2)*(u*(sin(v))-u))))>.38),-.45,0)"
2) For the fourth model (see last attached image), replace by:
"Tickness1= if(if(t=1,(abs(sin((N/2)*(u*abs(sin(v))-u))))<.4,(abs(sin((N/2)*(u*abs(sin(v))-u))))>.38),-.45,0)"
Enjoy!
MathMod script:
{
"Param3D": {
"Description ": ["(Inka Sun) and Carl SequinToroids models by Abderrahman Taha 15/10/2015"],
"Name": ["Inka Sun"],
"Component": ["Inka Sun1",
"Inka Sun2"],
"Const": ["cu=0.001",
"cv=0.001",
"N=3"],
"Funct": ["TicknessInkaSun= if(if(t=1,(abs(sin((N/2)*(u*(sin(v))-u))))<.4,(abs(sin((N/2)*(u*(sin(v))-u))))>.38),-.45,0)",
"TicknessSave= if(if(t=1,(abs(sin((N/2)*(u*abs(sin(v))-u))))<.4,(abs(sin((N/2)*(u*abs(sin(v))-u))))>.38),-.45,0)",
"Tickness1=if( t = 1, if ( (abs(sin((N/2)*u-v)))>.38,-.45,0),if ( (abs(sin((N/2)*u-v)))<.38,-.45,0))",
"Fx= (1+0.5*cos(u))*cos(v)",
"Fy=0.5*sin(u)",
"Fz= (1+0.5*cos(u))*sin(v)",
"DFxu= ((Fx(u,v,t)-Fx(u+cu,v,t))/cu)",
"DFxv= ((Fx(u,v,t)-Fx(u,v+cv,t))/cv)",
"DFyu= ((Fy(u,v,t)-Fy(u+cu,v,t))/cu)",
"DFyv= ((Fy(u,v,t)-Fy(u,v+cv,t))/cv)",
"DFzu= ((Fz(u,v,t)-Fz(u+cu,v,t))/cu)",
"DFzv= ((Fz(u,v,t)-Fz(u,v+cv,t))/cv)",
"n1= (DFyu(u,v,t)*DFzv(u,v,t)-DFzu(u,v,t)*DFyv(u,v,t))",
"n2= (DFzu(u,v,t)*DFxv(u,v,t)-DFxu(u,v,t)*DFzv(u,v,t))",
"n3= (DFxu(u,v,t)*DFyv(u,v,t)-DFyu(u,v,t)*DFxv(u,v,t))",
"R=sqrt(n1(u,v,t)^2+n2(u,v,t)^2+n3(u,v,t)^2)",
"Gx=Fx(u,v,t)+Tickness1(u,v,t)*n1(u,v,t)/R(u,v,t)",
"Gy=Fy(u,v,t)+Tickness1(u,v,t)*n2(u,v,t)/R(u,v,t)",
"Gz=Fz(u,v,t)+Tickness1(u,v,t)*n3(u,v,t)/R(u,v,t)"],
"Fx": ["Gx(u,v,1)",
"Gx(u,v,0)"],
"Fy": ["Gy(u,v,1)",
"Gy(u,v,0)"],
"Fz": ["Gz(u,v,1)",
"Gz(u,v,0)"],
"Umax": ["2*pi",
"2*pi"],
"Umin": ["0",
"0"],
"Vmax": ["2*pi",
"2*pi"],
"Vmin": ["0",
"0"]
}
}