HOME | DD
 cothe — Polynomial Variation
cothe — Polynomial Variation
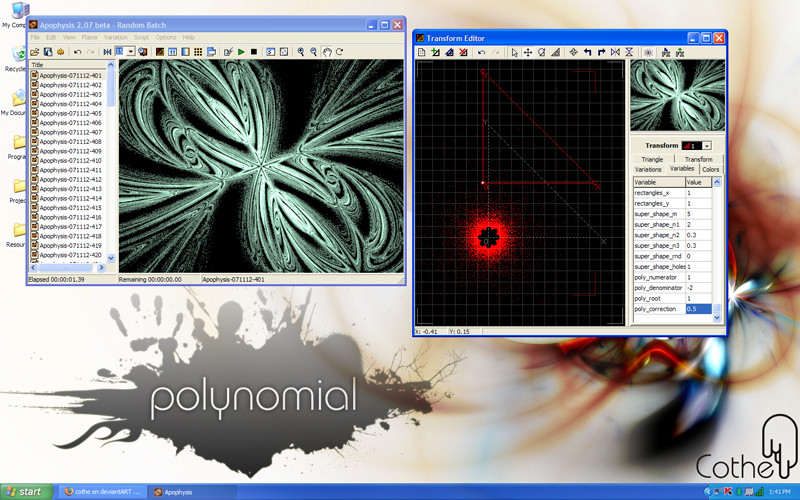
Published: 2007-11-12 23:41:49 +0000 UTC; Views: 6375; Favourites: 31; Downloads: 1290
Redirect to original
Description
Just to start off, if you guys end up making anything with this then please don't hesitate to let me know. I'd love to see what everybody can come up with.This is the plugin file for my Apophysis variation "Polynomial". To install, create a folder named "Plugins" in the directory that you keep your Apophysis executable in, put this file in that folder, and then run Apophysis. You must have Apo version 2.06 or higher in order to use plugins.
The Polynomial Variation seems to have some problems with other variation. I've looked into it quite a bit, and I can't find any obvious problem. Many times you will simply get a simple pop-up message, and after clicking okay you can simply resume what you were doing. Other times you will get an infinite number of pop-up messages, in which case you must use the Windows Task Manager to shut down Apophysis. It appears as though these problems are caused by conflicts with other variations, so you could try removing all your other plugins if you really want it to work.
I honestly have no idea what causes this, but I have never seen any permanent damage done by this variation. Still, use at your own risk.
The Polynomial treats the Apophysis 2D environment as the Complex Plane. Given that any point on the Complex plane can be expressed as the point "z", where "z = x + iy", then we can create functions using the variable "z". The Polynomial Variation uses the following function.
f(z) = z^(Numerator/Denominator)
Where "Numerator" and "Denominator" are specified variables which you can alter.
It should be noted that when the Numerator is divided by the Denominator, the resulting fraction is automatically reduced to lowest terms. Consequently, a Num of 6 and a Den of 4 is the same as a Num of 3 and a Den of 2.
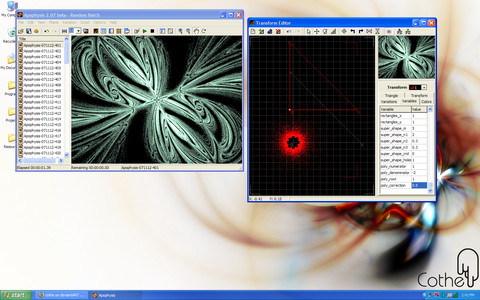
The Polynomial Variation also includes two extra variables, the Root variable, and the Correction variable.
Functions in which the Denominator variable is higher than 1 will yield multiple results. In fact, the value of the Denominator directly determines the number of roots that can be found (a Denominator of 2 will yield two roots, 3 will yield three roots, etc). If the value of the Root variable is set to 1 then all the roots will be shown. If the Root variable is set to 0, however, it will only show the root closest to the positive x-axis (or positive Real axis).
Examples of the Root variable in action can be found here:
[link]
[link]
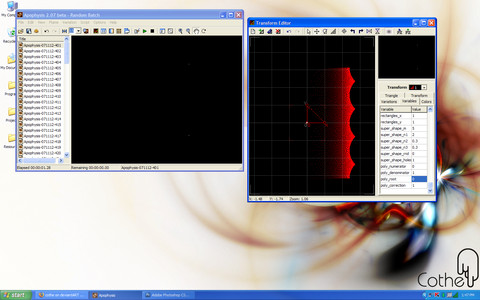
When the Numerator is larger than the Denominator then the points will begin to move very quickly away from the origin. On the flip side, if the Denominator is larger than the Numerator then points will begin to move very quickly towards the origin. To correct this (unless you want points that do that) you can use the Correction variable. If you have, for instance, a Num of 2 and a Den of 1, then you can set the Correction to 2 and it will modify the radius of the points so that they stay the same distance away from the center. Likewise, if your Den is 2 and your Num is 1, a Correction of 0.5 will stop points from going towards the center.
Example of the Correction variable can be found here:
[link]
[link]
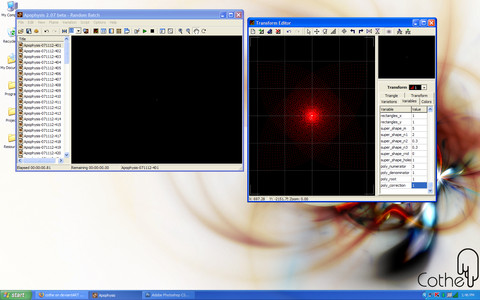
Another neat part of the Polynomial Variation is the built in Logarithmic function. When either the Numerator or Denominator (or both) are set to 0 then the function automatically becomes:
f(z) = ln(z)
This looks something like this.
[link]
Technically, the function should keep going on to infinity, both up and down. You can control the range of the y-coordinates by using the Root variable. This is demonstrated by these two images:
[link]
[link]
For those of you who are curious, many of the variations in Apophysis are actually tied into this kind of Polynomial function. I can demonstrate this with a few example.
First of all, the Spherical variation is actually very simple. It can be represented by the following function:
Spherical:
f(z) = z^(-1) = 1/z
As you might be able to guess, this can be emulated with the Polynomial Variation by simply setting either the Num or the Den to -1, and setting the other to 1. Now, because of the choice of the developers, the Spherical variation actually flips all the points over the x-axis, however the Polynomial Variation will still create a set of points that are a mirror image of the Spherical variation.
Another example is the Horseshoe variation. This variation uses the following formula:
Horseshoe:
f(z) = z^2
It then corrects the radius, just like the Polynomial variation can do, in order to stop points from going too far out. This can be emulated by setting the Num to 2, the Den to 1, and the Correction variable to 2.
Yet another example is the Julia variation. It uses the following formula:
Julia:
f(z) = z^(1/2) = sqrt(z)
It can be emulated by the Polynomial Variation by setting the Num to 1, and the Den to 2.
Lastly, the JuliaN variation can also be emulated. That variation uses the following formula:
JuliaN:
f(z) = z^(1/julian_power)
... and the julian_distance is used just like the Polynomial Variation's Correction variable. In order to emulate it, simply set the Num to 1, and the Den to whatever the julian_power is. Then, if the julian_distance is not 1, make sure the Correction variable is set equal to it.
If you need more help, you can check out my Scraps for 9 screenshots of the Polynomial Variation in action.
Related content
Comments: 17

This is brilliant, thank you so much. I will have a good study of this
👍: 0 ⏩: 0

Yeah, I was surprised that, based on the simplicity of just the idea of using an iterated Power function, nobody had really tried it in a program designed around an Iterated Function System...
👍: 0 ⏩: 1

what i was implying, is that people have, and i was pleased to find another
you can find a list of other coders, many of whom are working on fractals, in my older journal entry: [link]
👍: 0 ⏩: 1

I was referring to the Apophysis community, and the lack of a simple power function (which they really should have had since they implemented variables, not that I'm unthankful for what they have done), but I understand what your saying.
👍: 0 ⏩: 0

I've been really using this lately. This plugin made "Mandala of the Cherubim" and "Mandala of the Seraphim" quite beautiful. It also sometimes produces a really cool lacy effect at high zooms.
Thanks!
👍: 0 ⏩: 0

Dude, you're amazing. I honestly have a great amount of respect for people like you! Welcome to my watch list!
👍: 0 ⏩: 1

consider the hundreds of people who do these things routinely, and don't make a fuss about it
👍: 0 ⏩: 1

Awesome! Just plain awesome! Thanks for all the work you've put into this.
👍: 0 ⏩: 1

Thanks! I was just tired of having all these weird variations, and I figured it couldn't be that hard to make something that was simple, but could do a lot.
👍: 0 ⏩: 1

I've been trying to figure out how to make my own but each time someone tries pointing me in the right direction I get stuck... help?
👍: 0 ⏩: 1

You've got a copy of Delphi, right? You basically just need to use Delphi's DLL Wizard, and then reference the three main files (BaseVariation, GenericPluginDllFunc, and varWhatever). After that, you just change two things in GenericPluginDllFunc, and change around your variation file.
👍: 0 ⏩: 1

The program is incredibly expensive (I believe about $2,000). It's a miracle that I was actually in a position to get access to a computer that has it.
The other thing is that making a plugin uses almost nothing that Delphi has to offer, so it really isn't worth it to buy the software just for that.
As I say on my main page, if you want I can make you custom plugins for Apo. Note me with the appropriate information.
Usually it's as simple as...
x' = an expression
y' = an expression
... and I'll see what I can do.
👍: 0 ⏩: 0