HOME | DD
 FractalMonster — Diving into the Weird
by-nc-sa
FractalMonster — Diving into the Weird
by-nc-sa

#compass #exponent #play #formula
Published: 2019-05-07 10:24:20 +0000 UTC; Views: 474; Favourites: 26; Downloads: 6
Redirect to original
Description
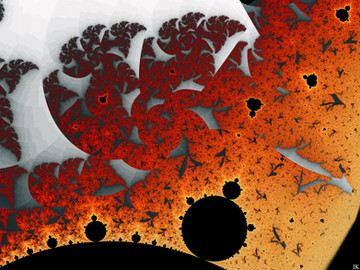
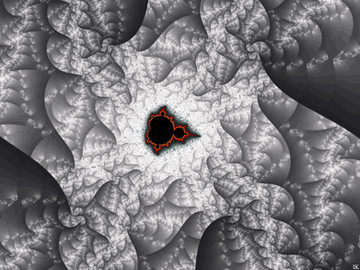
Further playing with the exponent in my compass formula, z -> z^d - da^(d-1) z. See my journal Fractal CompassesNow, my dear readers, I wanna promote the article,27) Compasses
in my Chaotic series. Along with this journal there are four deviations uploaded,
Compass_d=2
Compass_d=3
Compass_d=4
Compass_d=5
The “d” is the exponent in the iterated polynom p(z) = z^d - da^(d-1) z, the a-plane plotted and “z” initialized to the critical point z = +a. Why this formula is called the “Compass formula”? Well, just look at the above deviations, especially for d = 3 and higher






 For d = 3 we actually have z^3 - 3a^2 z whic
For d = 3 we actually have z^3 - 3a^2 z whic 






The exponent "d" in this motive is set to 1+i.
This is an in-zoom into the very tip of the previous .
Software: Ultra Fractal.
Formula: Extended Compasses (adding a parameter "b". the full parameter space becoming a four dimensional hyper space).
Below the UF parametr file. Play and have fun







DivingIntoTheWeird {
fractal:
title="Diving into the Weird" width=800 height=600 layers=1
credits="Ingvar Kullberg;4/22/2019"
layer:
caption="Background" opacity=100 method=multipass
mapping:
center=-5.37852829/9.227821865 magn=0.10872348
formula:
maxiter=10000 percheck=off filename="ik3.ufm"
entry="ExtendedCompasses" p_exponent=1/1
p_PlottedPlane="1.(a-real,a-imag)" p_hide=yes p_areal=0.0
p_aimag=0.0 p_breal=0.0 p_bimag=0.0 p_xrot=0.0 p_yrot=0.0
p_xrott=0.0 p_yrott=0.0 p_zrot=0.0 p_LocalRot=no p_diff=yes
p_bailout=10000000 p_dbailout=1E-15
inside:
transfer=none
outside:
density=0.1 transfer=linear
gradient:
smooth=yes rotation=-119 index=11 color=16579582 index=20
color=3026462 index=60 color=223 index=78 color=255 index=-243
color=57075 index=-32 color=16777212 index=-1 color=1709847
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 8

This is beautiful! I did look at your journal link about Fractal Compasses but you know the Math thing is completely over my head. 
👍: 0 ⏩: 1


.. and thanks Lea for the 
👍: 0 ⏩: 1

I have UF, I just don't ever do anything in it as when I have tried the tutorials, I get so terribly lost. I do what I think the tutorial means, step by step but do not get the same results. Clearly I have done something incorrect. However when I tried the tutorials before I always went back and forth between the tutorial and the work space in UF. Since I have a desktop computer now with dual monitors, (as well as several laptops), I have been thinking of trying UF again. I will check it out and go from there!
I appreciate your encouragement very much, Ingvar!
👍: 0 ⏩: 1

I never tried any tutorials myself ..
If you don't already have the actual formulas I'm using, download the zip,
klippan.seths.se/fractals/articles/modules.zip
and draw the formulas to My Document UF5 or UF6 or the version you have.
You also have a GetStarted manual there (written by me 
👍: 0 ⏩: 2

UF is not a program I can just wander around in and figure out. Most programs I am not able to do that. Usually if I can't figure it out, I don't do it because I don't understand tutorials. But I have tried to figure out UF off and on since 2004 and I guess I will give it another try because it really makes wonderful fractals!
👍: 0 ⏩: 1

Try to find out the boxes the correspond to to the boxes in FE ..
👍: 0 ⏩: 0

Awesome! I will do that! Thanks
👍: 0 ⏩: 1