HOME | DD
 FractalMonster — Golden Outbreaks
by-nc-sa
FractalMonster — Golden Outbreaks
by-nc-sa

#cubics #cbap
Published: 2016-01-25 14:13:22 +0000 UTC; Views: 1094; Favourites: 75; Downloads: 22
Redirect to original
Description
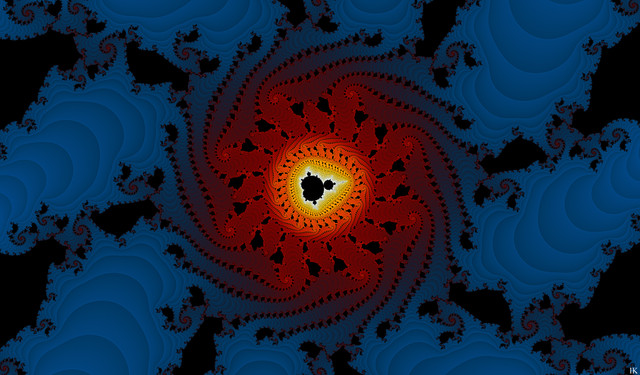
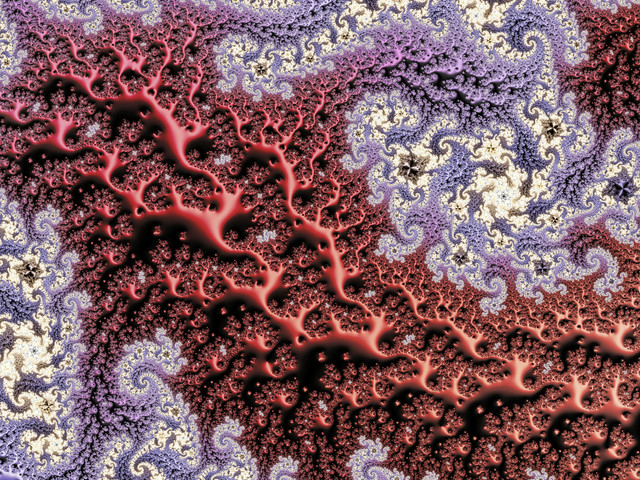
CBAP-cubics (When the other critical point is situated in a 2-periodic super attractive periodic cycle)Software: Ultra Fractal.
Formula: CBAP in the ik-module written by me. It's included in the zip that can be downloaded from here and also includes the modules of the great formula writer Greenseng her on dA
GoldenOutbreaks {
fractal:
title="Golden Outbreaks" width=1024 height=600 layers=1
credits="Ingvar Kullberg;1/23/2016"
layer:
caption="Layer 1" opacity=100 method=multipass
mapping:
center=0.000666106525096015/-2.6550990712235 magn=7500.5799
formula:
maxiter=25000 filename="ik.ufm" entry="CBAP" p_diff=no p_bailout=100
inside:
density=4 transfer=none filename="sp.ucl" entry="Log" f_func1=ident
p_k=1.0
outside:
transfer=linear filename="spr.ucl" entry="ContinousPotential"
p_auto=yes p_auton=5.0 p_n=5.0 p_numfact=2.0 p_scale=1.5 p_smooth=no
p_epsilon=0.5 p_illustr=no p_limiton=no p_limit=0.1 p_index3=0.0
p_index1=0.99 p_index2=0.0 p_speed=0.5 p_acc=1.0 p_clog=yes
p_power=3.0 p_reversed=no p_test=no p_testvalue=0.7 p_index4=0.29
gradient:
smooth=yes rotation=-159 index=8 color=16777197 index=97 color=43775
index=183 color=512 index=-160 color=6555392 index=-96
color=13331232
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 21

The perfection of the brokenness
👍: 0 ⏩: 0

I like this one a lot! The pattern is awesome
👍: 0 ⏩: 1

You like one of my raw fractals 

👍: 0 ⏩: 1

A little, but I don't know much. Care to tell me more about them?
👍: 0 ⏩: 1

OK 


👍: 0 ⏩: 1

I saw your note! Thanks a lot!
👍: 0 ⏩: 1

You apparently did
👍: 0 ⏩: 0

Super beautiful 
👍: 0 ⏩: 1

So we have the same opinion 

👍: 0 ⏩: 0

Maybe you are right 

👍: 0 ⏩: 0