HOME | DD
 TheInflater — Game Design: Path Finding
TheInflater — Game Design: Path Finding
Published: 2013-05-07 14:42:11 +0000 UTC; Views: 1461; Favourites: 0; Downloads: 0
Redirect to original
Description
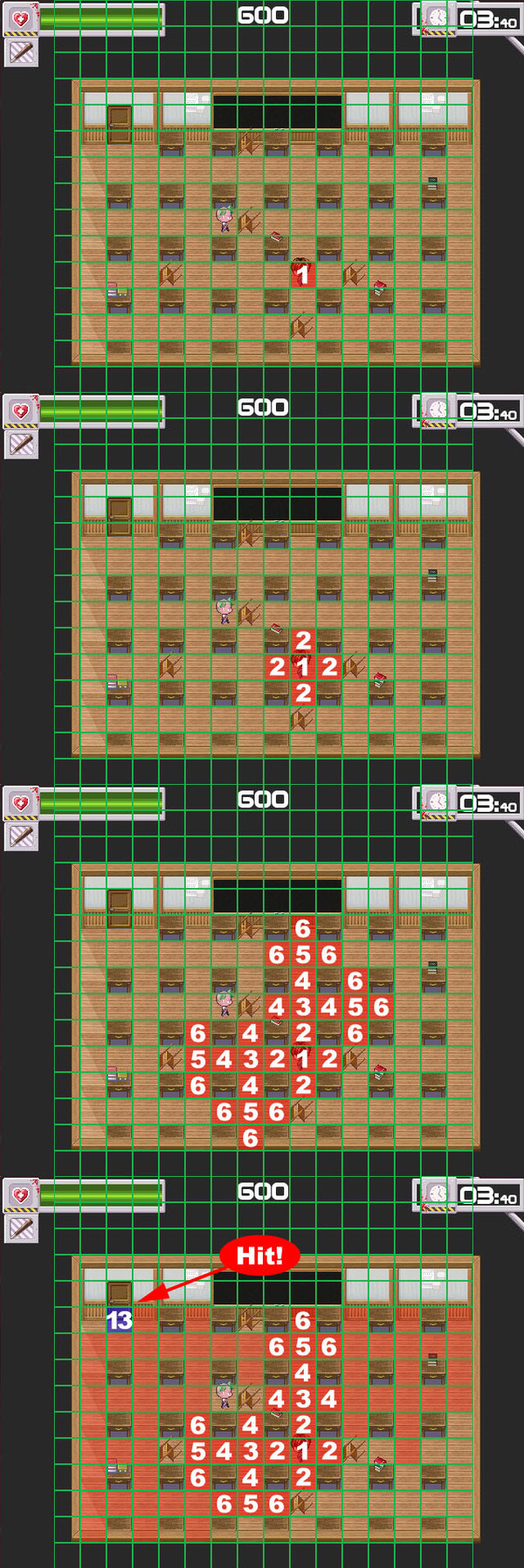
Little explanation of how to implement a Path Finding algorithm for a game design. The game is fromFarraj
and you can find it in his profile.
Related content
Comments: 4

I implemented such an algorithm, when I was coding on Pascal (for some kind of contest) and then in my attempt to make a C&C clone. I found that this is horribly inefficient algorithm. It makes sense only in the complex maze, but in a relatively big and open map with several obstacles it consumes memory and CPU in horrible quantities.
👍: 0 ⏩: 1

Well ... efficient is - in terms of game programming - what makes it fast. This one has two loops to loop through a two-dimensional array with just some very basic and simple tests. You can unroll the loop by implementing the game grid into a one-dimensional array which makes it even faster.
Any other »more intelligent« algorithm will check for more cases. Those checks could - maybe - take more time than just this simple loop.
It would be interesting to know why you skipped this type of algorithm.
👍: 0 ⏩: 1

Because its performance in large mostly open spaces it takes around O(N^3) if N is size.
Consider another algorithm: go towards the target if possible. If the direct route is blocked, split the runner in two and try to sidestep the blocking obstacle. Go round it clockwise and counterclokwise (checking two possible directions which is shorter we don't know, until we reach the aim). Once runner can go towards the target - stop going round the obstacle, and go towards target until next obstacle is blocking, then split again.
+.1 it can reach the target in O(N) if there is no obstacles, or very few.
+.2 no need to use a lot of extra memory (O(number of runners))
-.1 found path is not guaranteed to be shortest.
-.2 in a very complex maze performance may be comparable or even worse than of floodfill pathfinder.
👍: 0 ⏩: 1

Well ... in theory it sounds better. There are many many implementation things that needs to be solved when using your algorithm:
a) What's »go directly to the target«?
Taking the picture above a direct route would be a diagonal line from the »1«-point to the door. Which means: several steps up and several steps to the left in a specific order. You have to calculate those.
b) Sidestepping an obstacle
By splitting the path from the point where an obstacle exist you have to calculate point a) again for the two splits. You also have to implement some sort of a stack or maybe a connected list to store those values and to memorize you now have new paths. And of course values if the path splits again and again and so on. You also have to take care to not overflow a stack/list with those values.
c) Path ends
You also have to delete the paths if they can't go further and can't split. which means you have to implement a delete-routine in of the paths in the stack/list.
d) Number of extra paths
Your solution sounds good if there is some sort of a direct path to the exit. Now consider some sort of a maze where the route takes a lot of »go in the opposite direction first«. You method would mean a lot of splits of the path before you reach the goal.
Which leads to ...
e) Unpredictable memory amount
With that stack/list it's hard to predict the amount of memory you actually need for worst case situations.
That's a lot - and I mean A LOT - of extra things to calculate and to consider for every little step of the player. Again: My solution is very simple to implement and predictable.
If you like I can come up with a C/Java-code example which will show how simple it is.
👍: 0 ⏩: 0















