HOME | DD
 Donitz — Digital circuit: Binary adder
Donitz — Digital circuit: Binary adder

Published: 2011-04-29 14:14:16 +0000 UTC; Views: 4866; Favourites: 18; Downloads: 95
Redirect to original
Description
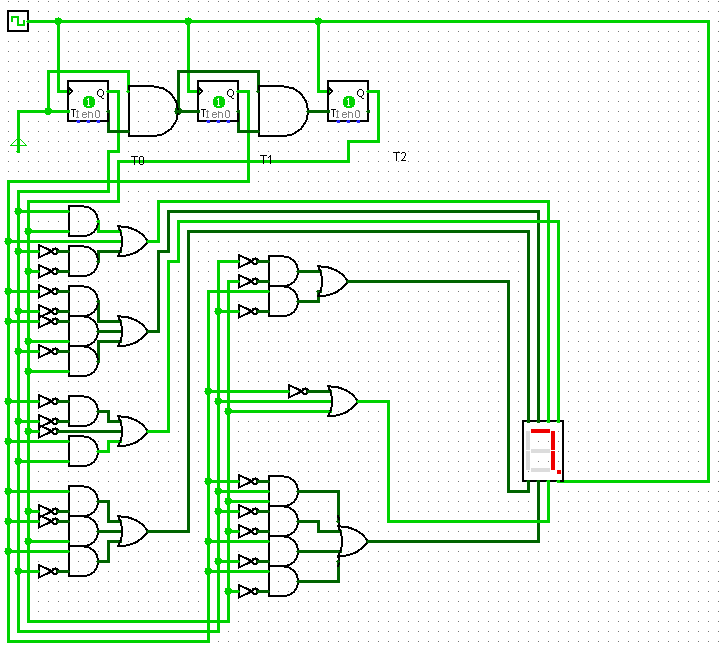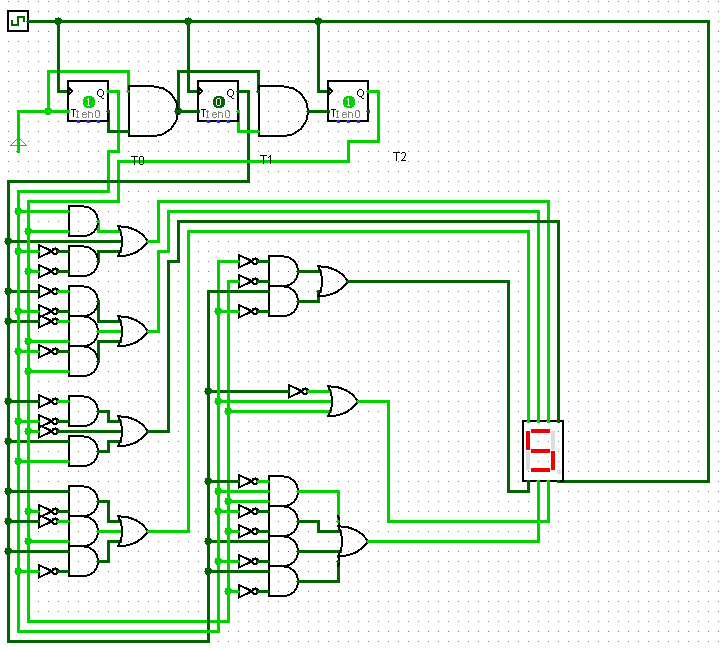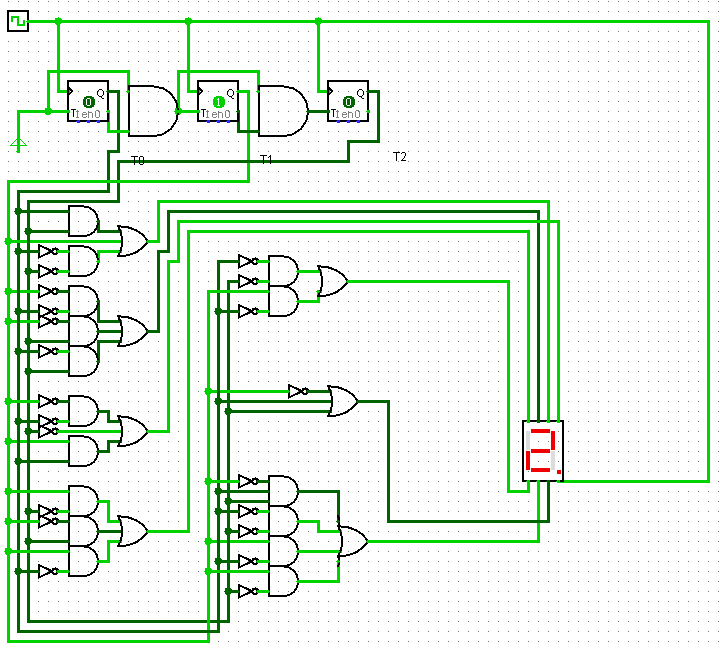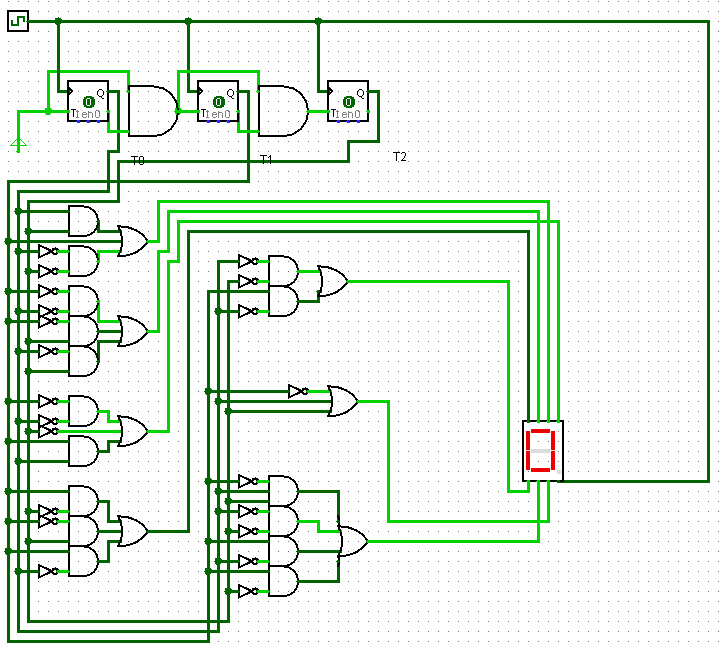
Okay, I may know some stuff about Boolean logic, but as far as digital circuits go I am pretty much clueless how to implement them properly. This was all just an improvisation done for an unrealistic simulation in flash.Use the keypad down to the left to add a number, but be patient because the logic (especially the binary-coded decimal converter) works very slowly and it will take a little while for the result to turn up on the LCD display.
The propagation delay is highly exaggerated as each tick can cause a single state change in each gate.
This means that it will for example always take exactly two updates for two gates in series to propagate a signal. This also leads to an interesting situation where the flip-flops (bit storage) can remain in a metastable state indefinitely, as you can see wherever the circuits are flashing.
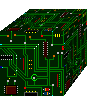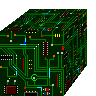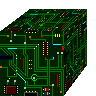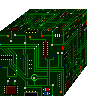
This circuit adds two numbers together using nothing but NAND and NOT gates.
A NAND gate gives a low output if both its inputs are high; else it will give a high output. A NOT gate simply reverses the input for the output. A NOT gate could easily be produced from a NAND gate by connecting together the NAND gates inputs to a single input. This would seriously waste a lot of space in the circuit image so instead I treat each blue NAND gate as a not gate if it only has 1 input.
The gate's (blue) inputs are to the left and right of the pixel, and the output is either above or below it.
Wires are yellow, bridges (where two wires can cross) are purple, and buttons are red.
Some common structures that you can find in the circuit are flip-flops, small borderless squares that can store a single bit. I usually put these in pairs so to prevent their last value to affect the new input value.
There are also several binary adders, large green boxes. These add two binary numbers together and can be connected in series to handle infinitely large binary numbers. Similarly there are binary subtractors up in the corner, smaller green boxes. Also you can find a 2 to 4 and a 4 to 16 decoder in a couple of places.
I’d love to hear your opinion on this circuit, suggestions and criticisms are most welcome.
Related content
Comments: 9

i think that you would love the Powder Game.
but my god this is slow.
👍: 0 ⏩: 0

There should be a download link to the side. Ask if you want the source but it's basically just a huge image with some simple logic behind it.
👍: 0 ⏩: 1

what software app did you use for it (what will run a swf file)
thanks its awesome
👍: 0 ⏩: 1

Amazing stuff here. I have no idea how to do this IRL, never mind in flash!
👍: 0 ⏩: 0