HOME | DD
 FractalMonster — The Crack of the Common Set
by-nc-sa
FractalMonster — The Crack of the Common Set
by-nc-sa
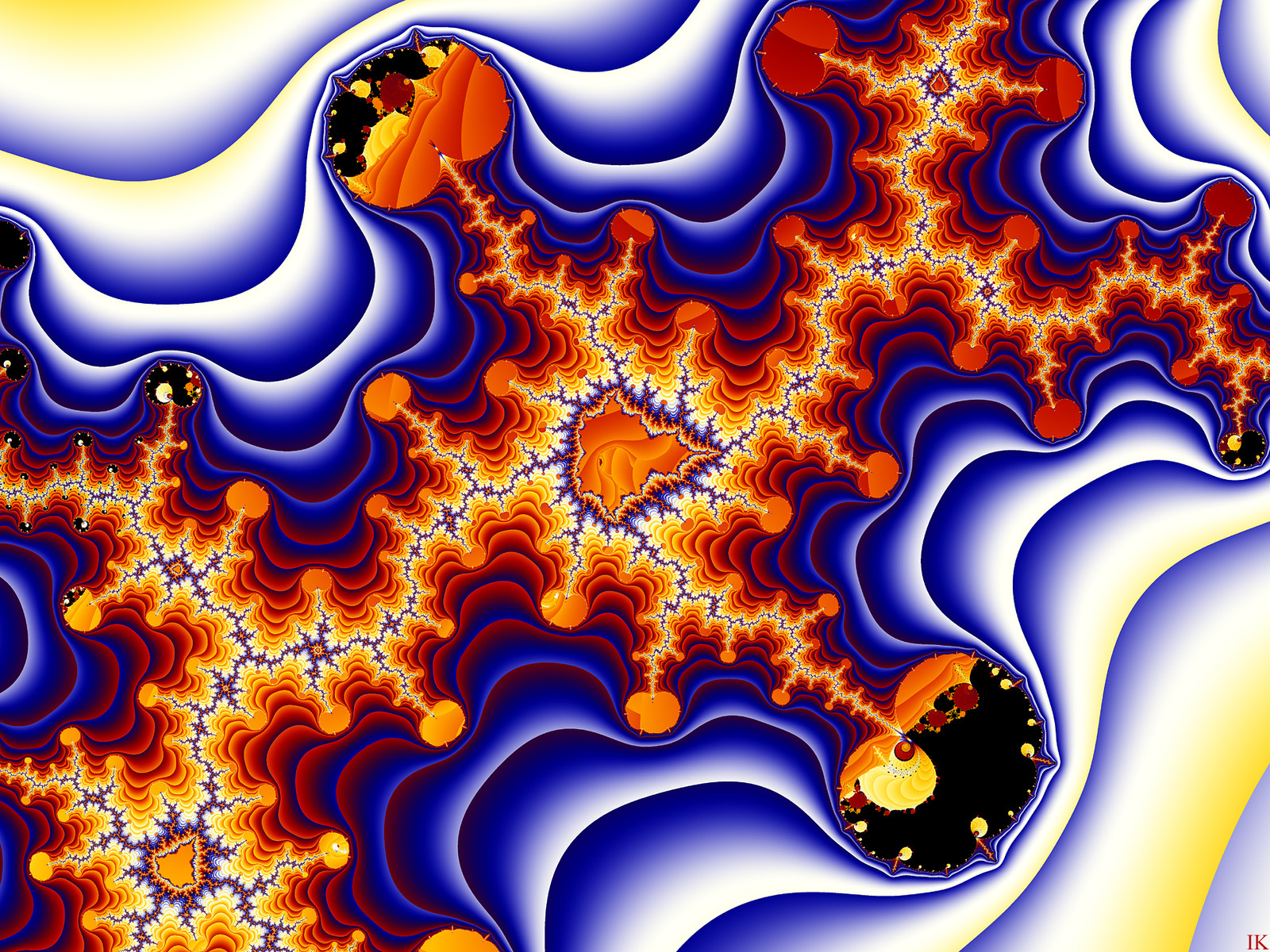
#quartic #parameterspace
Published: 2018-05-22 10:27:12 +0000 UTC; Views: 626; Favourites: 46; Downloads: 11
Redirect to original
Description
The branch leading up to the earlier deviation .Quartic Parameter Space. See my journal Quartics Revisited.
Ultra Fractal6
Below the parameter file. Play and have fun







TheCrackOfTheCommonSet {
fractal:
title="The Crack of the Common Set" width=800 height=600 layers=1
credits="Ingvar Kullberg;5/15/2018"
layer:
caption="QCL" opacity=100 method=multipass
mapping:
center=-0.450504166631/0.304849444449 magn=904.97737
formula:
maxiter=50000 filename="sp3.ufm" entry="QuarticParameterspace3"
p_PlottedPlane="1.(a-real,a-imag)" p_M=QCL p_SetBorders=no
p_hide=yes p_areal=0.0 p_aimag=0.0 p_breal=0.0 p_bimag=0.5
p_creal=0.0 p_cimag=0.0 p_xrot=0.0 p_yrot=0.0 p_xrott=0.0
p_yrott=0.0 p_xrotu=0.0 p_yrotu=0.0 p_xrotv=0.0 p_yrotv=0.0
p_zrot=0.0 p_LocalRot=no p_diff=no p_bailout=100.0 p_dbailout=1E-6
inside:
transfer=none
outside:
density=4 transfer=linear filename="spr.ucl"
entry="ContinousPotential" p_auto=yes p_auton=2.0 p_n=5.0
p_numfact=5.0 p_scale=1.0 p_smooth=no p_epsilon=0.5 p_illustr=no
p_limiton=no p_limit=0.1 p_index3=0.0 p_index1=0.99 p_index2=0.0
p_speed=0.5 p_acc=1.0 p_clog=yes p_power=4.0 p_reversed=no p_test=no
p_testvalue=0.7 p_index4=0.29
gradient:
smooth=yes rotation=199 index=499 color=156 index=199 color=8716288
index=299 color=16121855 index=399 color=46591
opacity:
smooth=no index=0 opacity=255
}
Related content
Comments: 20

(If any of the external links below don't open, right click them!)
Maybe you would appreciate my Chaotic series of fractal articles (<- click) if you have a little theoretical interest
Regarding deep zooms in the Mandelbrot set, if you check out my deviation Cauliflowerfort and click the link under "Artist's Comments", from page 4 you can follow the entire zoom sequence in 28 steps
In this journal you have some links to cool fractal animations I stumbled over at YouTube. Also check out the zoom videos in this journal
.. and from the middle of the nineties there is a fantastic TV program about fractals, Colors of Infinity by Arthur Clarke 
👍: 0 ⏩: 1

Thanks for the info...I’ll give them all a try...!! 🦊
👍: 0 ⏩: 1

No probs, really glad if you obtain some inspiration
👍: 0 ⏩: 0


.. and thanks for the 
👍: 0 ⏩: 1

We will see, more will come 
IF you wanna try some free simple fractal software of "Mandel an Julia" type, go to this journal. You don't need to know the math behind
Maybe you would appreciate my Chaotic series of fractal articles (<- click) if you have a little theoretical interest
👍: 0 ⏩: 1

I will, but how to be a core member?
👍: 0 ⏩: 1

Somewhere in the upper menu on your profile side
👍: 0 ⏩: 0

Maybe 


.. and thanks for the 
👍: 0 ⏩: 1

no never, i ll Google It
👍: 0 ⏩: 1

Fractals are patterns that repeat themselves (or have details) at every level of magnification 

👍: 0 ⏩: 0


.. and thanks for the 
👍: 0 ⏩: 1

è stato un piacere ^^
👍: 0 ⏩: 0