HOME | DD
 pillemaster — Cutting, Slicing and Scaling Tutorial
pillemaster — Cutting, Slicing and Scaling Tutorial
Published: 2012-04-30 11:17:05 +0000 UTC; Views: 2357; Favourites: 23; Downloads: 189
Redirect to original
Description
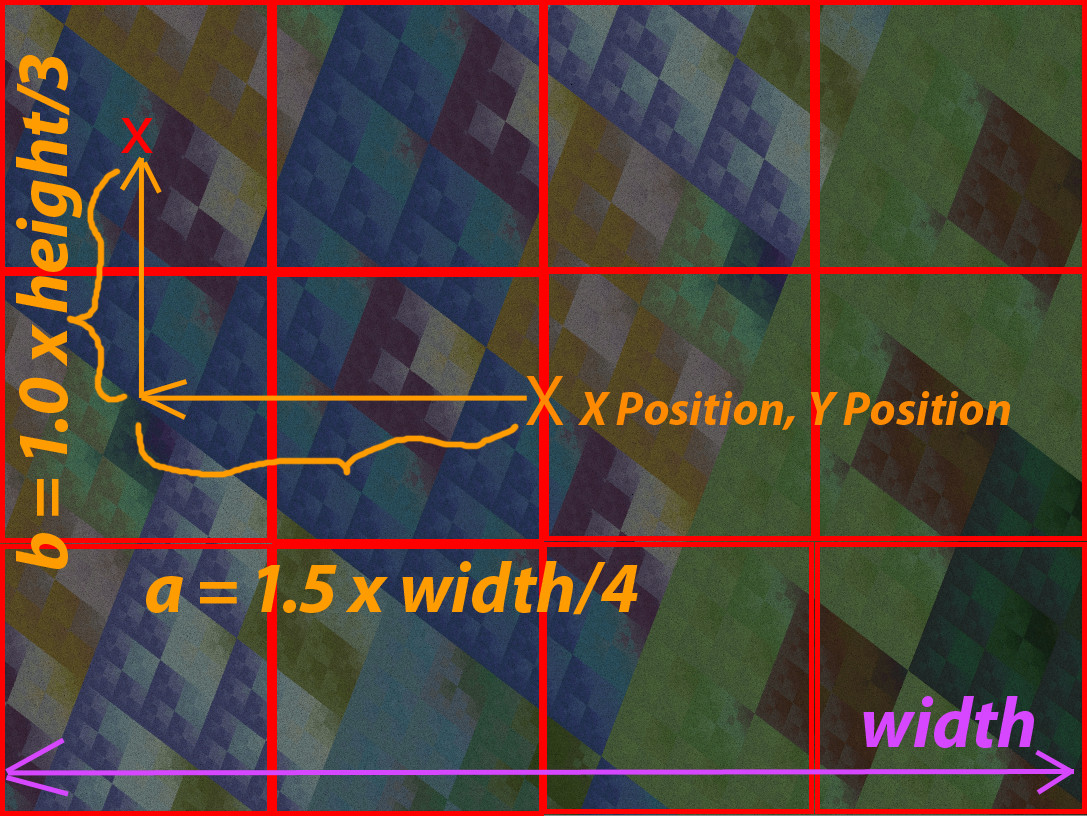
Tutorial about rendering Apophysis flames in huge dimensions by cutting and slicing the image into fitting subimages.Hope it helps since the available scripts on this topic seem to cause some problems with rotation and flames, using post transforms... and it is not possible to subdivide a picture into a matrix of squares
please ... see as well
p.s.: it would be great if anybody could write a script for that ... since my programming skill is not the best
Related content
Comments: 17

I found it just now. Love it ! It will certainly make my half-grey cell work overtime 

👍: 0 ⏩: 0


👍: 0 ⏩: 1

i have some problems with the slicing method - never get fitting pars for some reasom ... probaply my fault
👍: 0 ⏩: 0

Wow, this looks pretty complicated! Funny, I've been working on the script for what I've termed "patchwork rendering" (that is, squares). Just seem to have cracked it today - same technique to remove all X, Y and rotation as before. Any problems with this is most likely due to misreading the instructions - it's not the simplest thing to explain! There are also potential problems with mixed installations of Apo 7X (32 + 64 bit). If you had no problems with the strips, you're welcome to try the patchwork method before I release it.
P.S. I've used it successfully with chaotica in batch mode to render a 7680 x 5760 px image as 12 1920 px squares
👍: 0 ⏩: 1

cool! sure i wouls certainly like to try it - the tutorial just describes the method i've used so far ... take a look it is not as complicated as it seems
👍: 0 ⏩: 1

I think it's the number of decimal places that comes as rather a shock to the reader! I shall study it if my head feels suitably clear. Here's my method + script [link]
👍: 0 ⏩: 2

your script works well ... the method (manual rotation of the final xform ...) is a somewhat complicated ... but just the other way around than mine ... please take a look at my excel file (especially the formulas) ... it might help to create a perfectly working new script
👍: 0 ⏩: 1

Perhaps it's how I explain it that makes the rotation seem complicated. It summarises to 5 steps:
- select post xform of final xform
- copy and paste rotation from Camera tab into rotation field of Triangle tab
- remove rotation on Camera tab (double-click)
- switch to World pivot
- click Rotate triangle counter-clockwise
Hadn't realised your pack had a spreadsheet as I still use Office 2002. I managed to download a compatibility pack to convert it - now I understand the decimal places!
If I can work out a formula for converting rotations to coordinates (perhaps your spreadsheet will help!), I could script the whole process in one. One thing I have missed out is the possibility that the starting flame has a non-zero zoom. Probably the simplest way around that is to 'neutralise' the zoom by a change of scale before performing the positional calculations.
👍: 0 ⏩: 1

reading is not my strength^^ so missed the thing with the switch to world pivot ... thought is ment post transform or something ... i must confess i never used it until a few days ago... but it workes nicely
i'm pretty sure the resulting script will be cool
... let me know if you need any help with the spread sheet or to figure out what i was doing
👍: 0 ⏩: 2

No worries, I've found a way: convert the original x,y positions to polar coordinates, add the rotation angle then back-convert to x,y, based on r remaining constant. Now to get it scripted...
👍: 0 ⏩: 0

Well, if you can easily deduce a formula to convert counter-clockwise rotation of the 3 xform coordinates about the 'World' origin, that would save me loads of effort! Specifically, how does a rotation through theta degrees transform the x,y coordinates of each of the O, X, Y points of the triangle in terms of trigonometric functions? I see you use combinations of sin and cos in the spreadsheet, so I'm sure it's possible
👍: 0 ⏩: 1

cool - good luck with the scripting!
👍: 0 ⏩: 0

thank you i downloaded it and will test it as soon as possible ... but we have great weather here...
👍: 0 ⏩: 0